[解決済み] nで割り切れる2進数の文字列を受け付けるDFAを設計する。

質問

任意の数 'n' が与えられたとき、10進数で 'n' で割り切れる数の2進文字列 {0, 1} を受け入れるような DFA を設計する方法を知りたいです。

異なる'n'のための異なるDFAがあるでしょうが、誰かが私が任意の数0 < n < 10を続行するために従うべき基本的なアプローチを与えることができます。

どのように解決するのですか？

以下に、私が書いた答えは n が 5 の場合の答えを書いていますが、同じ方法で n と「任意の位置の数システム」、例えば2進数、3進数...に対してDFAを描くことができます。

最初に「完全なDFA」という用語に傾き、A DFA 完全な領域で定義された をδ:Q × Σ→Qで定義したものを「Complete DFA」と呼びます。言い換えれば、完全DFAの遷移図には欠落したエッジがない（例えばQの各状態から、Σの各言語記号に対して1つの出射エッジが存在する）、と言うことができるのです。注：あるときは 部分的 DFAをδ⊆Q×Σ→Qと定義することがある（読む。 DFAの定義で「δ:Q × Σ→Q」はどう読むか ).

数'n'で割り切れる2進数を受け付けるDFAを設計せよ。

ステップ-1 : ある数ωをある数で割るとき n で割ったとき、余りは 0, 1, ..., (n - 2) または (n - 1) のいずれかになる。もし余りが 0 で割り切れることを意味します。 n で割り切れるかどうかです。ということで、私のDFAでは、状態q _r となり、これは余りの値 r に対応するもので、ここで 0 <= r <= (n - 1) であり、DFAの総状態数は n .

数列ωをΣ上で処理した後の終了状態は、q _r は、ω % n => r (% reminder operator)を意味する。

オートマトンにおいて、状態の目的は記憶要素のようなものである。例えば扇風機のスイッチのように、扇風機がオフなのかオンなのかが分かるような情報です。n = 5の場合、DFAの5つの状態は5つの記憶情報に対応し、以下のようになります。

1. 状態q ₀ リマインダが0であれば到達する状態。 <サブ 0 は最終状態である(accepting state)。また、初期状態でもある。
2. 状態q <サブ 1 は、リマインダが1であれば、非最終状態になる。
3. 状態 q ₂ リマインダが2の場合、非終了状態。
4. 状態 q ₃ リマインダが3の場合、非終了状態。
5. 状態 q ₄ reminder が 4 の場合、非終了状態。

以上の情報を使って、以下のように5つの状態の遷移図TDを描き始めることができます。

<ブロッククオート

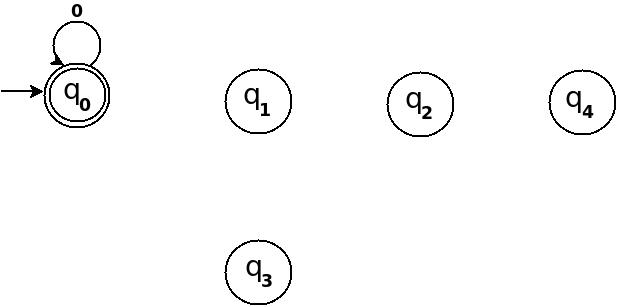
図-1

つまり、5つの余りの値に対して5つの状態。文字列ωを処理した後、終了状態がqになった場合 ₀ となれば、入力文字列の10進数換算値が5で割り切れることを意味する。 ₀ は最終的に2つの同心円としてマークされる。

さらに、遷移規則δ:(q ₀ , 0)→q ₀ をシンボルの自己ループとして '0' 状態qで ₀ これは，文字列の10進数表記が '0' は 0 であり，0 は n .

ステップ-2 : 上記の TD は不完全で、以下の文字列のみを処理することができます。 '0' s. そこで、さらにエッジを追加して、それ以降の番号の文字列を処理できるようにする。下の表は、次のステップで追加できる新しい遷移規則を示しています。

│

番号

│

バイナリ

│

残部(%5)

│

終了状態

│

│一│一│一│q
<サブ

1

       │

│二 │十 │二 │q
<サブ

2

       │

│三 │11 │三 │q
<サブ

3

       │

│フォー │100 │4 │q
<サブ


4

       │
└──────┴──────┴─────────────┴─────────┘

1. バイナリ文字列を処理する場合 '1' という遷移規則δ:(q)があるはずです。 <サブ 0 , 1)→q <サブ 1
2. 2：-2進法表現は '10' であるべきで、エンドステートはq <サブ 2 を処理すること。 '10' という遷移規則δ:(q)を追加するだけでよい。 <サブ 1 , 0)→q <サブ 2
   
   パス : →(q <サブ 0 )─1→(q <サブ 1 )─0→(q <サブ 2 )
3. 3：-バイナリーでは '11' であり、エンドステートはq <サブ 3 という遷移規則δ:(q)を追加する必要がある。 <サブ 1 , 1)→q <サブ 3
   
   パス : →(q <サブ 0 )─1→(q <サブ 1 )─1→(q <サブ 3 )
4. 4：-バイナリで '100' であり、エンドステートはq <サブ 4 . TDはすでにプレフィックス文字列を処理しています '10' を追加するだけで、新しい遷移規則δ:(q <サブ 2 , 0)→q <サブ 4
   
   パス : →(q <サブ 0 )─1→(q <サブ 1 )─0→(q <サブ 2 )─0→(q <サブ 4 )

<イグ 図-2

ステップ3 : ファイブ＝101

図-2 の遷移図はまだ不完全で、多くのエッジが欠落しています。 <サブ 2 , 1)- ? . といった文字列を処理するルールが存在するはずです。 '101' .

なぜなら '101' = 5は5で割り切れる、と認めること。 '101' を追加しますδ:(q <サブ 2 , 1)→q <サブ 0 を図-2に示します。

パス →(q <サブ 0 )─1→(q <サブ 1 )─0→(q <サブ 2 )─1→(q <サブ 0 )

この新ルールにより、遷移図は以下のようになります。

図-3

以下、各ステップで次の2進数を選び、「完全なDFA」であるTDを得るまで、欠けたエッジを追加していきます。

ステップ4 6＝110である。

処理することができます。 '11' を図-3の現在のTDに示す。→(q <サブ 0 )─11→(q <サブ 3 ) ─0→( ? ). 6 % 5 = 1なので、これは1つのルールδ:(q)を追加することを意味します。 <サブ 3 , 0)→q <サブ 1 .

図-4

ステップ-5 セブン＝111

│

番号

│

バイナリ

│

残部(%5)

│

終了状態

│

 パス

       │ 

追加

       │

セブン │111 │7 % 5 = 2 │q
<サブ

2

       │ q
<サブ

0

─11→q
<サブ

3


│

 q
<サブ

3

─1→q
<サブ

2

    │

図-5

ステップ6 エイト＝1000

│

番号

│

バイナリ

│

残部(%5)

│

終了状態

│

 パス

     │ 

追加

     │
├──────┼──────┼─────────────┼─────────┼──────────┼─────────┤
エイト │1000 │8 % 5 = 3 │q
<サブ

3

       │q
<サブ

0

─100→q
<サブ

4

 │ q
<サブ

4

─0→q
<サブ

3

  │

図-6

ステップ-7 : ナイン＝1001

│

番号

│

バイナリ

│

残部(%5)

│

終了状態

│

 パス

     │ 

追加

     │
├──────┼──────┼─────────────┼─────────┼──────────┼─────────┤
9 │1001 │9 % 5 = 4 │q

<サブ

4

       │q
<サブ

0

─100→q
<サブ

4

 │ q
<サブ

4

─1→q
<サブ

4

  │
└──────┴──────┴─────────────┴─────────┴──────────┴─────────┘

図-7

TD-7では、エッジの総数は10==Q×Σ=5×2である。そして、10進数で5で割り切れるすべての2進文字列を受け入れることができる完全なDFAである。

数nで割り切れる3進数を受け付けるDFAを設計する。

ステップ1 バイナリーの場合と全く同じで、figure-1 を使用します。

ステップ-2 ゼロ、ワン、ツーを追加

│

10進数

│

三元的

│

残部(%5)

│

終了状態

│

   追加

        │
├───────┼───────┼─────────────┼─────────┼──────────────┤
│ゼロ │q0 │δ：（q0,0）→q0│。
├───────┼───────┼─────────────┼─────────┼──────────────┤
│一│q1│δ:(q0,1)→q1│││││││││││││││││││││││。
├───────┼───────┼─────────────┼─────────┼──────────────┤
│2 │q2 │ δ:(q0,2)→q3 │ δ
└───────┴───────┴─────────────┴─────────┴──────────────┘

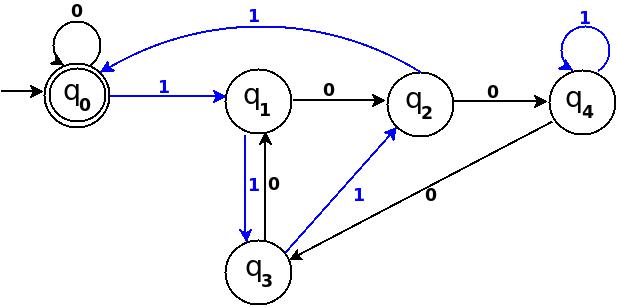
図-8

ステップ3 3、4、5を追加

│

10進数

│

三元的

│

残部(%5)

│

終了状態

│  

追加

        │
├───────┼───────┼─────────────┼─────────┼─────────────┤
│三 │十 │q3 │δ：（q1,0）→q3 │δ：（q1,0）→q3│。
├───────┼───────┼─────────────┼─────────┼─────────────┤
四 │11 │4 │δ：（q1,1）→q4 │δ：（q1,1）→q4│。
├───────┼───────┼─────────────┼─────────┼─────────────┤
│五│十二│q0│δ:(q1,2)→q0││││││││││││││││││││││││││。
└───────┴───────┴─────────────┴─────────┴─────────────┘

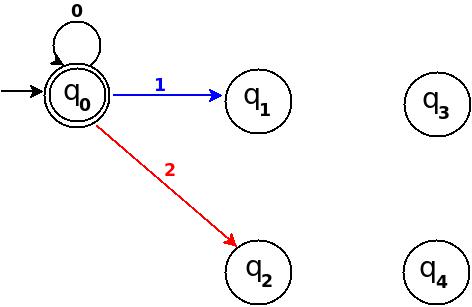
図-9

ステップ4 6、7、8を追加

│

10進数

│

三元的

│

残部(%5)

│

終了状態

│  

追加

        │
├───────┼───────┼─────────────┼─────────┼─────────────┤
六 │二十 │q1 │δ：（q2，0）→q1 │。
├───────┼───────┼─────────────┼─────────┼─────────────┤
セブン │21 │2 │δ：(q2,1)→q2 │。
├───────┼───────┼─────────────┼─────────┼─────────────┤
エイト │22 │q3 │δ：（q2,2）→q3 │δ：（q2,2）→q3│。
└───────┴───────┴─────────────┴─────────┴─────────────┘

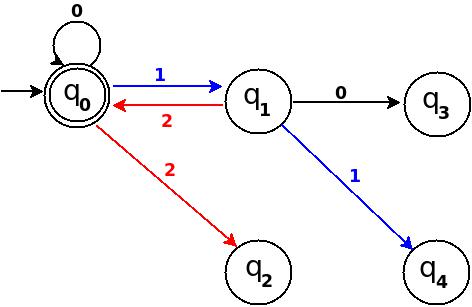
図-10

ステップ-5 9、10、11を追加

│

10進数

│

三元的

│

残部(%5)

│

終了状態

│  

追加

        │
├───────┼───────┼─────────────┼─────────┼─────────────┤
│Nine │100 │4 │q4 │ δ:(q3,0)→q4
├───────┼───────┼─────────────┼─────────┼─────────────┤
十 │101 │0 │δ：（q3,1）→q0│。
├───────┼───────┼─────────────┼─────────┼─────────────┤
イレブン │102 │1 │δ：(q3,2)→q1│。
└───────┴───────┴─────────────┴─────────┴─────────────┘

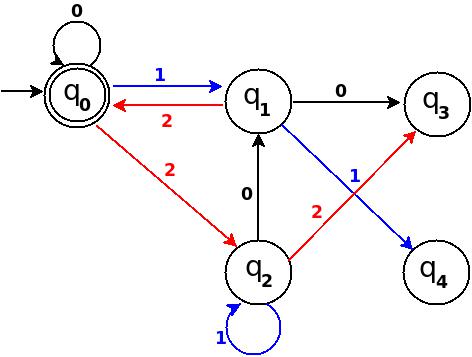
図-11

ステップ6 Add Twelve, Thirteen, Fourteen（12、13、14を加える

┌────────┬───────┬─────────────┬─────────┬─────────────┐
│

10進数

 │

三元的

│

残部(%5)

│

終了状態

│  

追加

        │
├────────┼───────┼─────────────┼─────────┼─────────────┤
│Twelve │110 │q2 │ δ:(q4,0)→q2 │ δ
├────────┼───────┼─────────────┼─────────┼─────────────┤
什器│111│q3│ δ:(q4,1)→q3│ δ:(q4,1)→q4,1)
├────────┼───────┼─────────────┼─────────┼─────────────┤
フォーティーン│112 │q4 │ δ:(q4,2)→q4 │ δ:(q4,2)→q4 │ δ:(q4,2)
└────────┴───────┴─────────────┴─────────┴─────────────┘

<ブロッククオート <ブロッククオート

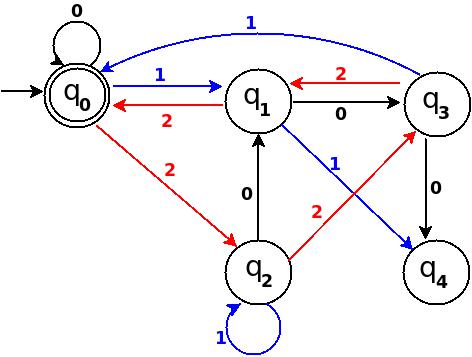
図-12

遷移図figure-12の辺の総数は15 = Q × Σ = 5 * 3（完全なDFA）である。そして、このDFAは{0,1,2}上の文字列のうち、10進数で5で割り切れるものをすべて受け入れることができる。

各ステップにおいて、表に3つの項目があることに気づけば、それは各ステップにおいて、完全なDFAを作るために状態から出る可能性のあるすべてのエッジを追加するからである（そして、エッジを追加してq _r となるようにエッジを追加します）。 r )!

さらに付け加えると、2つの正規表現の和もまた正規表現であることを思い出してください。10進数で3か5で割り切れる2進文字列を受け付けるDFAを設計する必要がある場合、3と5で割り切れるDFAを別々に作成し、両方のDFAを結合して目的のDFAを構築します（1 <= n <= 10の場合、10のDFAを結合する必要があります）。

10進数で5と3で割り切れるような2進文字列を受け付けるDFAを作れと言われたら、15で割り切れるDFAを探していることになります（でも6と8はどうでしょう）。

注：この手法で描かれたDFAは、以下の場合にのみ最小化されたDFAになります。 がない場合のみです。 の間に共通因子がある場合のみ、DFAを最小化することができます。 n と基底の間の共通因子はありません。 いいえ は存在しない。したがって、上で作ったDFAは両方とも最小化DFAである。もし興味があれば、数のミニ状態についてさらに読むことができる n と基底 b は論文を読んでください。 分割可能性と状態の複雑さ .

^{Pythonのライブラリpygraphvizの勉強をしながら、遊びで書いたPythonスクリプトを下に追加しました。 何かの参考になればと思い、追加しています。}

数「n」で割り切れる基本数「b」文字列のDFAを設計せよ。

というわけで、上記のトリックを応用して、任意の底の数列を認識するDFAを描くことができます。 'b' で、与えられた数で割り切れるものは 'n' . そのDFAでは、状態の総数が n (となります。 n の場合）、エッジの数は 'b' * 'n' に等しくなければなりません - それは完全なDFAです： 'b' = DFAの言語のシンボルの数、 'n' = 状態の数。

上記のトリックを使って、入力に対してDFAを描画するPythonスクリプトを以下に書いてみました。 base と number . スクリプトでは、関数 divided_by_N は、DFAの遷移規則を base * number の各ステップにおいて 各ステップ番号において、私は num を数字文字列に変換する。 num_s 関数を使って baseN() . 各数字列を処理するのを避けるために、一時的なデータ構造である lookup_table . 各ステップで、数値文字列に対する終了状態 num_s は評価され lookup_table に格納され、次のステップで使用されます。

DFAの遷移グラフのために、私は関数 draw_transition_graph を使って Pygraphvizライブラリ (非常に使いやすい)を使用しています。このスクリプトを使用するには、以下のものをインストールする必要があります。 graphviz . 遷移図にカラフルなエッジを追加するために、各シンボルに対してランダムにカラーコードを生成しています。 get_color_dict という関数を用いている。

#!/usr/bin/env python
import pygraphviz as pgv
from pprint import pprint
from random import choice as rchoice

def baseN(n, b, syms="0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ"):
    """ converts a number `n` into base `b` string """
    return ((n == 0) and syms[0]) or (
        baseN(n//b, b, syms).lstrip(syms[0]) + syms[n % b])

def divided_by_N(number, base):
    """
    constructs DFA that accepts given `base` number strings
    those are divisible by a given `number`
    """
    ACCEPTING_STATE = START_STATE = '0'
    SYMBOL_0 = '0'
    dfa = {
        str(from_state): {
            str(symbol): 'to_state' for symbol in range(base)
        }
        for from_state in range(number)
    }
    dfa[START_STATE][SYMBOL_0] = ACCEPTING_STATE
    # `lookup_table` keeps track: 'number string' -->[dfa]--> 'end_state'
    lookup_table = { SYMBOL_0: ACCEPTING_STATE }.setdefault
    for num in range(number * base):
        end_state = str(num % number)
        num_s = baseN(num, base)
        before_end_state = lookup_table(num_s[:-1], START_STATE)
        dfa[before_end_state][num_s[-1]] = end_state
        lookup_table(num_s, end_state)
    return dfa

def symcolrhexcodes(symbols):
    """
    returns dict of color codes mapped with alphabets symbol in symbols
    """
    return {
        symbol: '#'+''.join([
            rchoice("8A6C2B590D1F4E37") for _ in "FFFFFF"
        ])
        for symbol in symbols
    }

def draw_transition_graph(dfa, filename="filename"):
    ACCEPTING_STATE = START_STATE = '0'
    colors = symcolrhexcodes(dfa[START_STATE].keys())
    # draw transition graph
    tg = pgv.AGraph(strict=False, directed=True, decorate=True)
    for from_state in dfa:
        for symbol, to_state in dfa[from_state].iteritems():
            tg.add_edge("Q%s"%from_state, "Q%s"%to_state,
                        label=symbol, color=colors[symbol],
                        fontcolor=colors[symbol])

    # add intial edge from an invisible node!
    tg.add_node('null', shape='plaintext', label='start')
    tg.add_edge('null', "Q%s"%START_STATE,)

    # make end acception state as 'doublecircle'
    tg.get_node("Q%s"%ACCEPTING_STATE).attr['shape'] = 'doublecircle'
    tg.draw(filename, prog='circo')
    tg.close()

def print_transition_table(dfa):
    print("DFA accepting number string in base '%(base)s' "
            "those are divisible by '%(number)s':" % {
                'base': len(dfa['0']),
                'number': len(dfa),})
    pprint(dfa)

if __name__ == "__main__":
    number = input ("Enter NUMBER: ")
    base = input ("Enter BASE of number system: ")
    dfa = divided_by_N(number, base)

    print_transition_table(dfa)
    draw_transition_graph(dfa)

実行します。

~/study/divide-5/script$ python script.py 
Enter NUMBER: 5
Enter BASE of number system: 4
DFA accepting number string in base '4' those are divisible by '5':
{'0': {'0': '0', '1': '1', '2': '2', '3': '3'},
 '1': {'0': '4', '1': '0', '2': '1', '3': '2'},
 '2': {'0': '3', '1': '4', '2': '0', '3': '1'},
 '3': {'0': '2', '1': '3', '2': '4', '3': '0'},
 '4': {'0': '1', '1': '2', '2': '3', '3': '4'}}
~/study/divide-5/script$ ls
script.py filename.png
~/study/divide-5/script$ display filename

出力します。

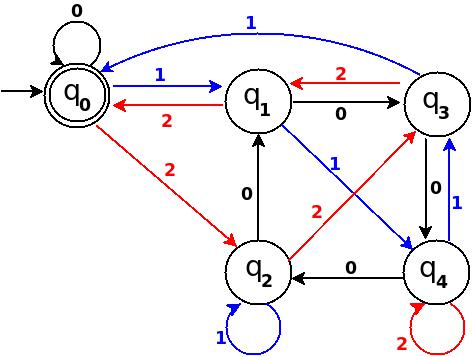
DFAは5で割り切れる基数4の文字列を受け付けます。

同様に、base = 4 と number = 7 を入力すると - が生成されます。 dfa は '7' で割り切れる '4' 基数の文字列を受け付けます。

このとき filename を .png または .jpeg .

<sub>このスクリプトを書くために使用するものを参照します。

➊機能 baseN から pythonで整数を文字列に変換します。

➋ pygraphvizをインストールする。 "Pythonはpygraphviz"を見ません。

➎ Pygraphvizの使い方を知る。 Python-FSM"

➍ 各言語記号のランダムな16進カラーコードを生成する。 .joinとforループを使ってランダムな16桁のコード生成器を作るにはどうしたらいいですか？</sub>