の前に書いてください。

最短経路問題は、グラフ理論の研究における古典的なアルゴリズム問題である。
グラフ（ノードとパスからなる）において、2つのノード間の最短経路を求めることを目的とする。

今回は主に、最短経路問題を解くためのmatlabアプリを提供することです。

今回共有する最短経路問題アプリは無向グラフのみで、実際には一方通行の存在により、実際の問題は有向グラフであることが多く、有向グラフの内容については後ほど紹介します。

2つの表現

隣接行列方式と隣接表方式。

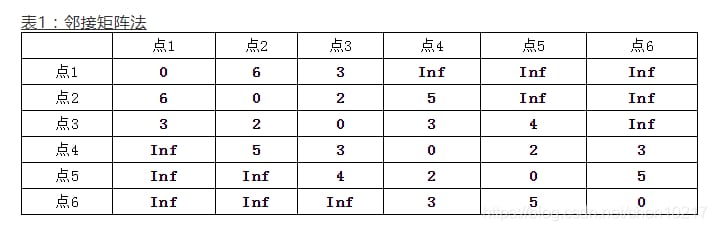
Adjacency Matrixは、頂点間の隣接関係を表す行列である。

隣接行列は、有向グラフ隣接行列と無向グラフ隣接行列に分けられる。無向グラフの隣接行列は対称でなければならないが、有向グラフの隣接行列は必ずしも対称でなくてもよい。

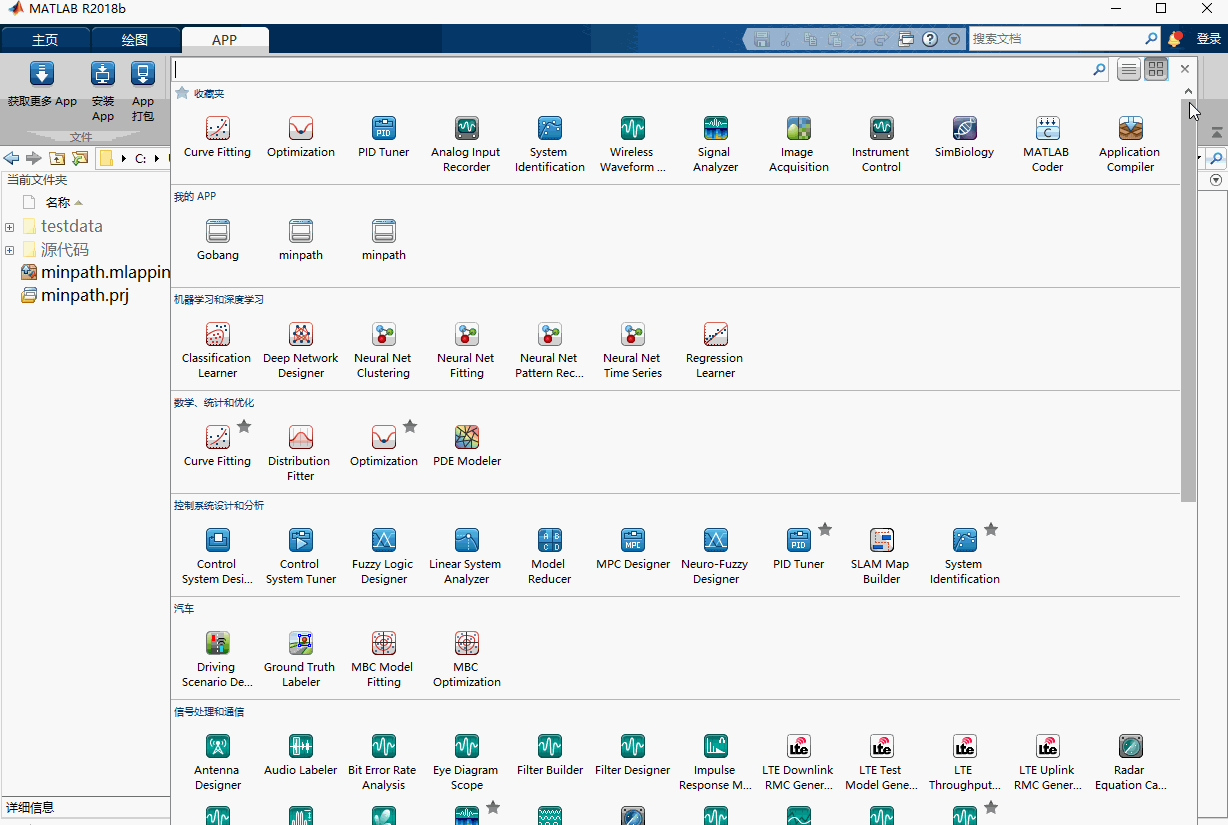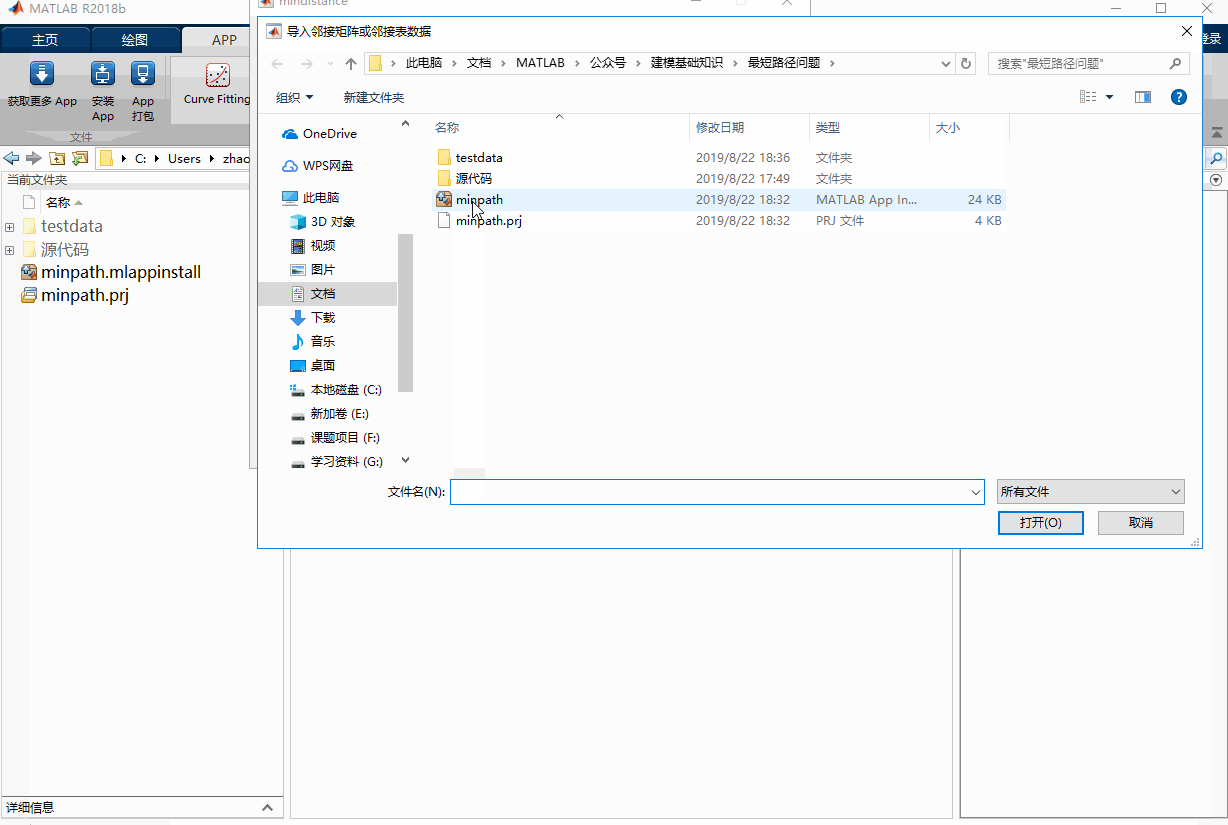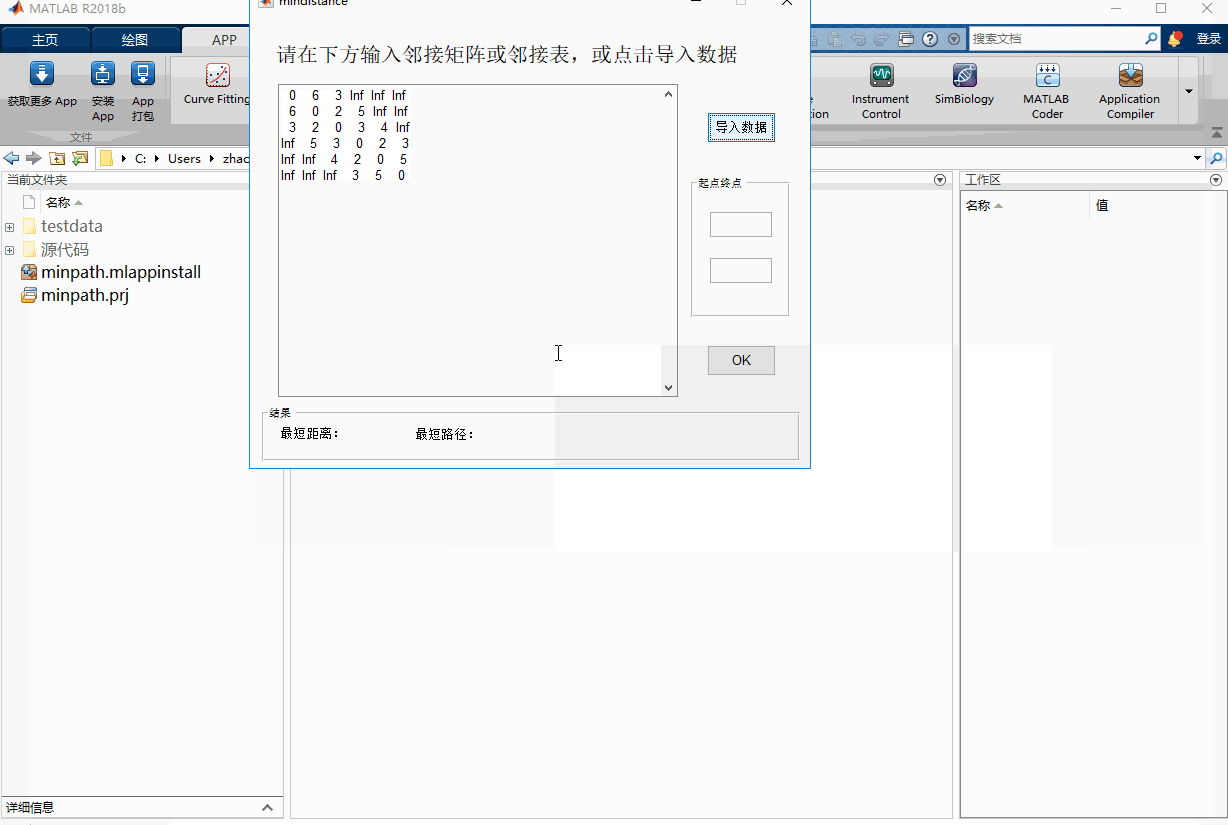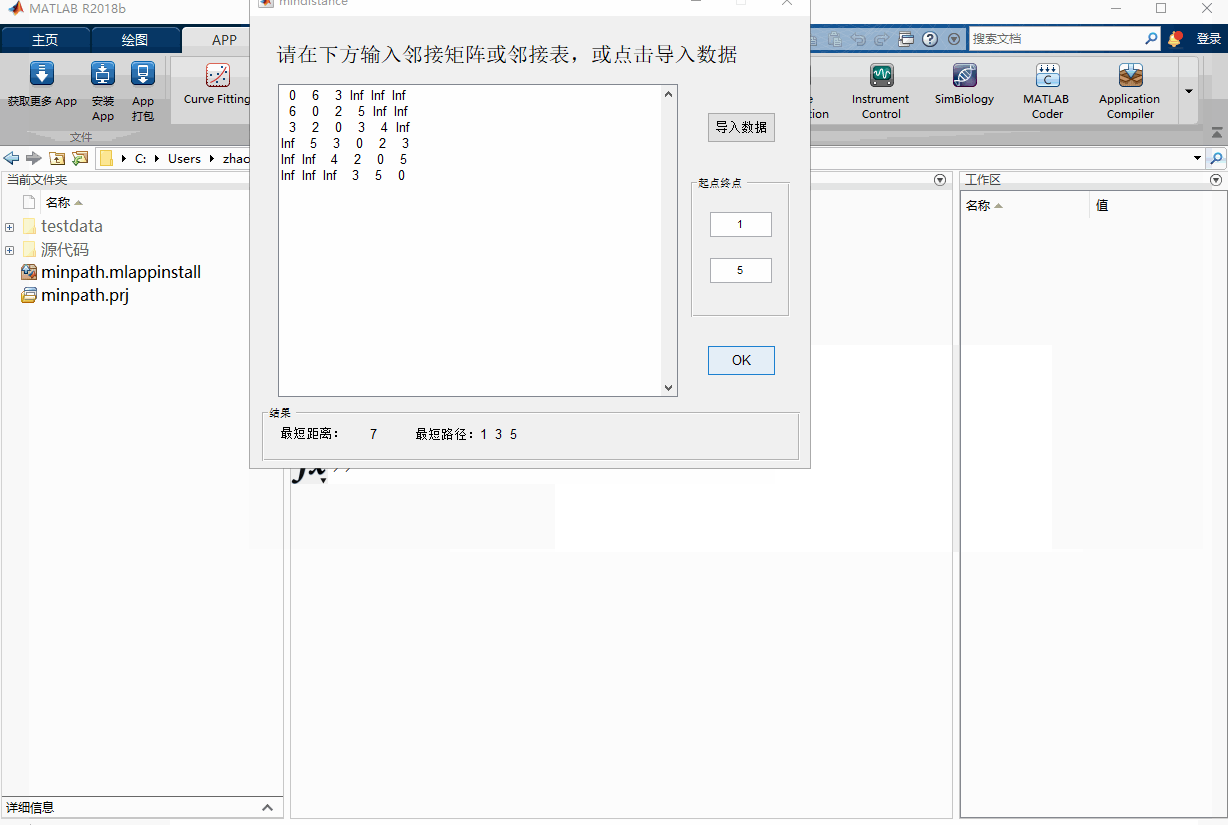
ここでは、無向グラフの隣接行列を用いて、図1の位置と道路の関係を表現している。例えば、場所1と場所2の距離を6とすると、表1の行列は、1行目2列目、2行目1列目ともに6という値を持つ。ロケーション1とロケーション4の間には道路がなく、その行列は無限大Infとして表され、ロケーション1は自分との距離が0である。

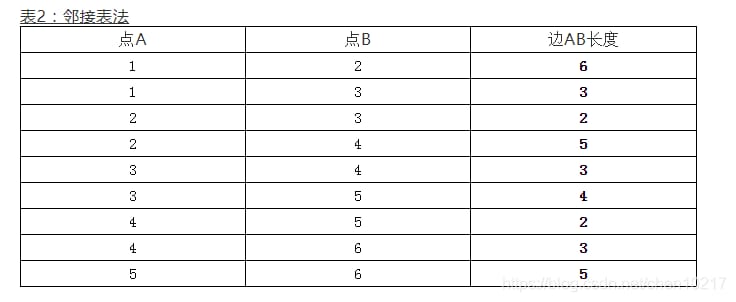
隣接表は、グラフに存在するエッジとその長さだけを保存する。例えば、点1と点2の間に長さ6のエッジが存在する場合、隣接表には1, 2, 6の行が存在することになる。

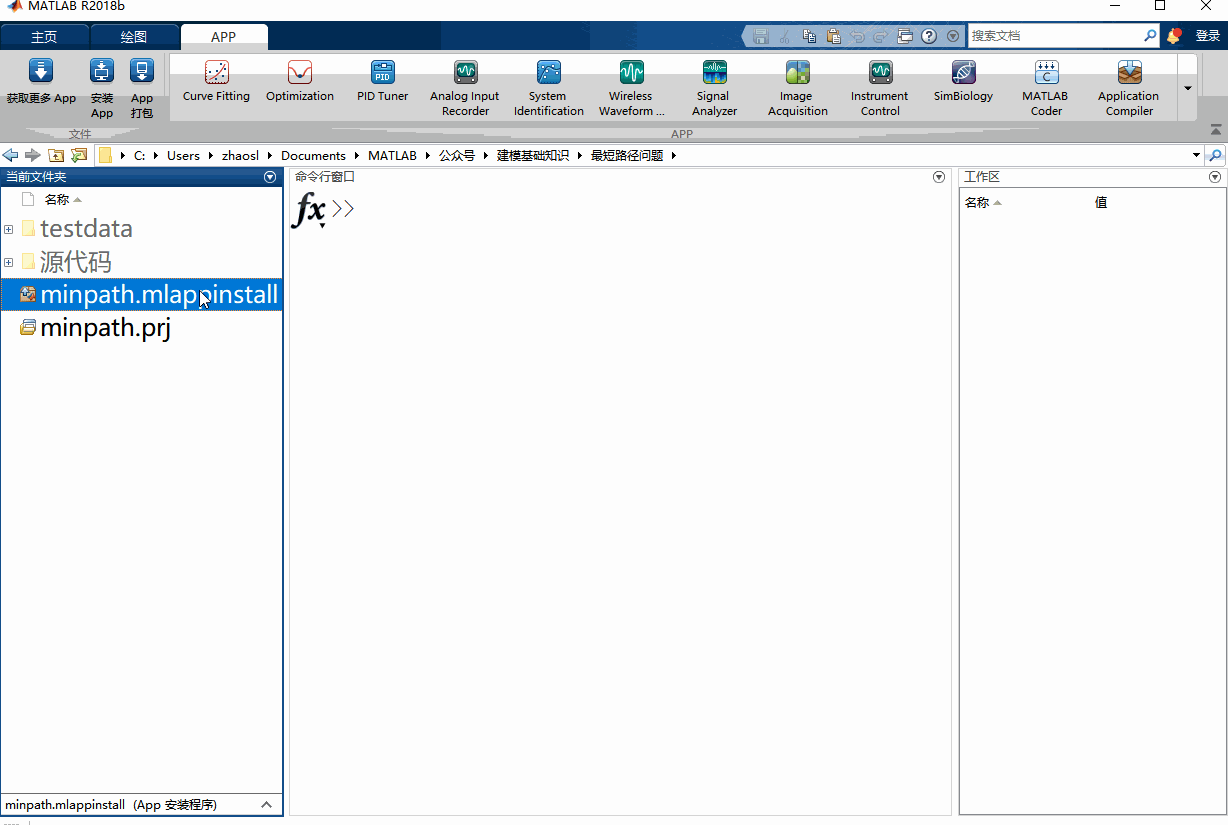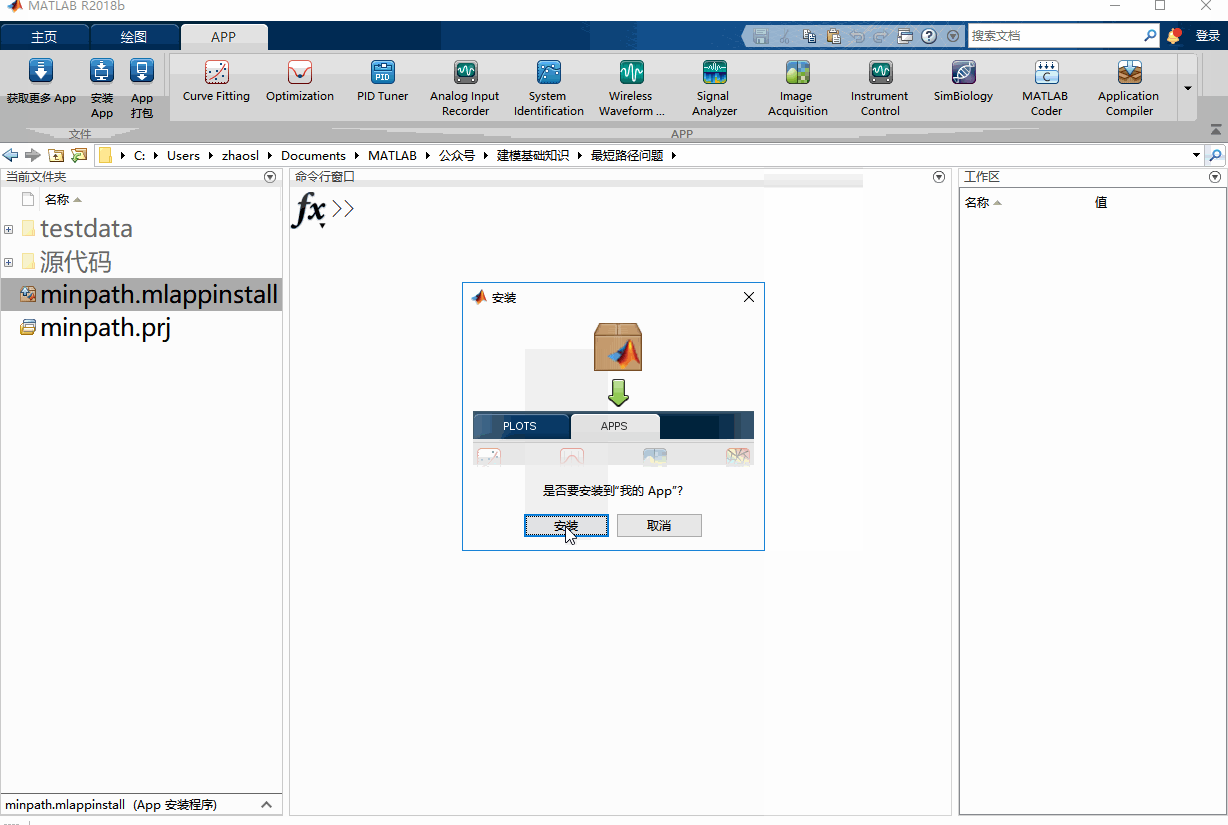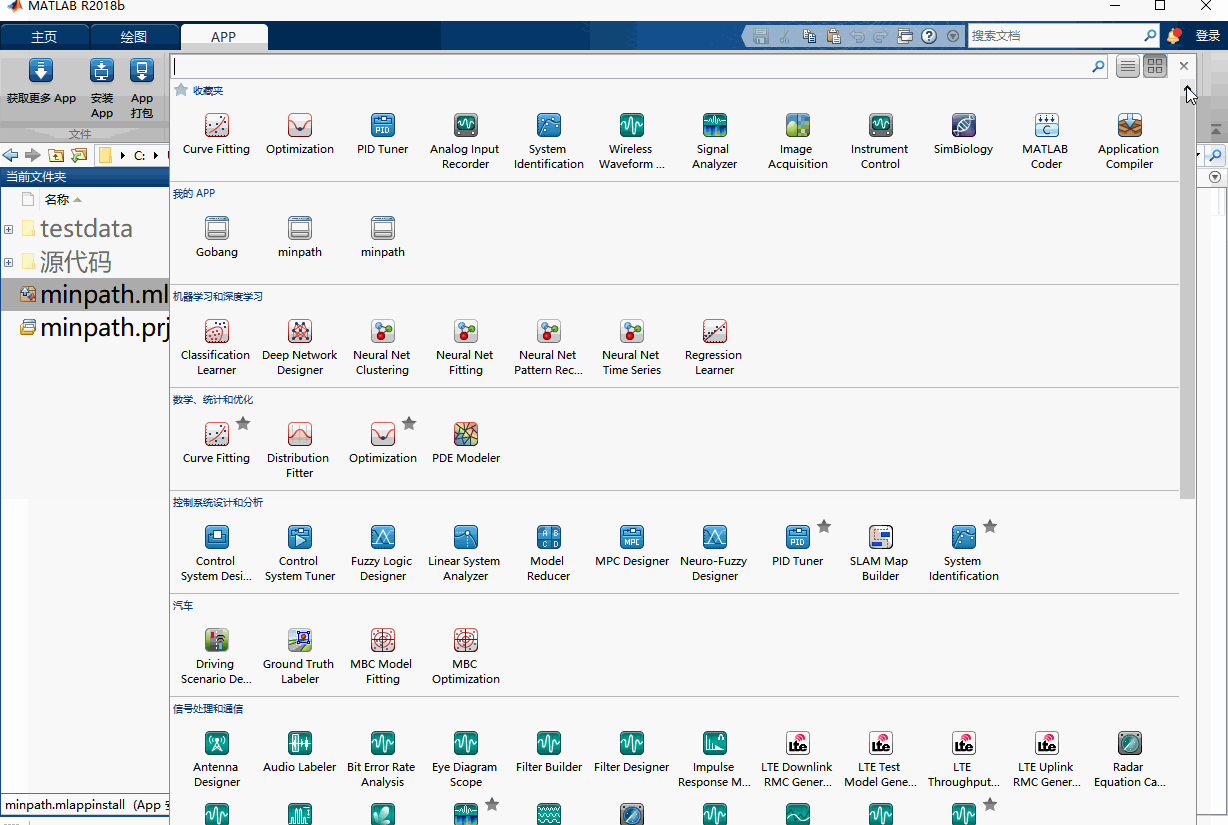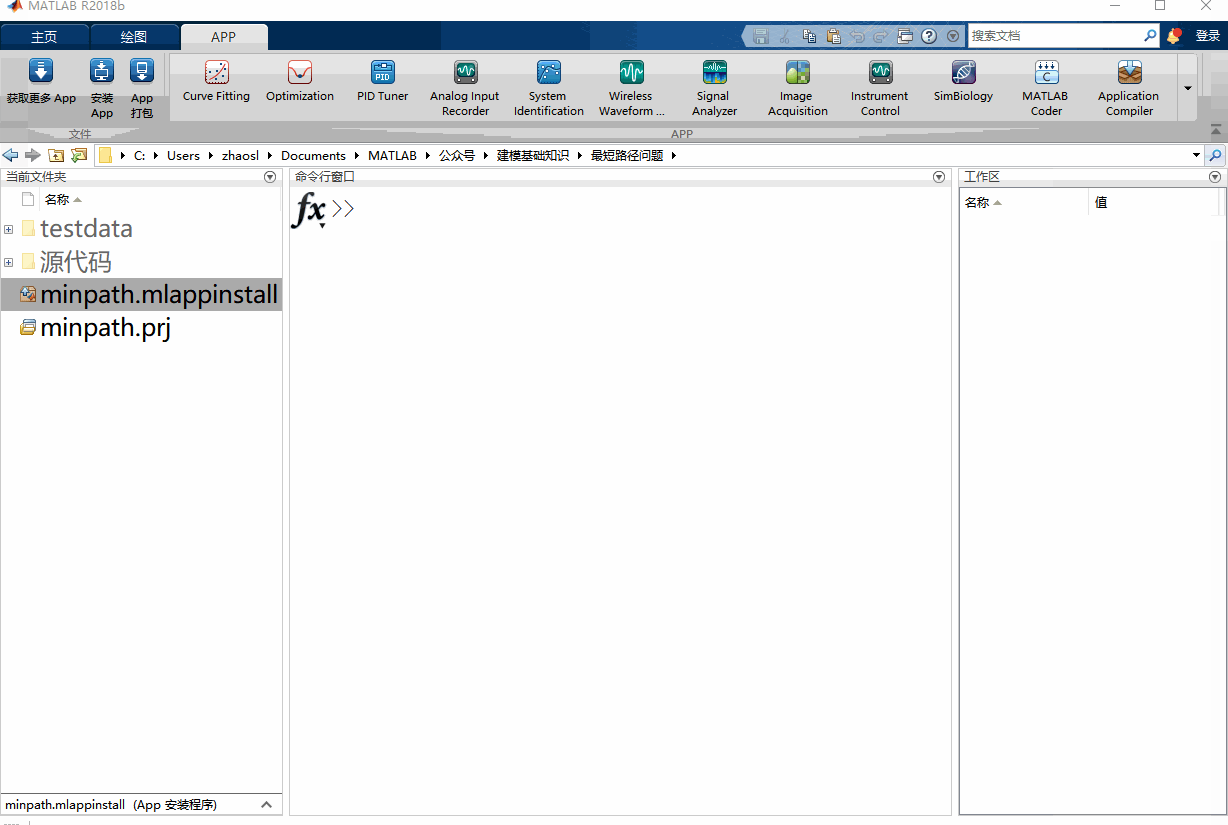
minpathのインストール

matlabのカレントパスの中で、minpath.mlappinstallをダブルクリックするとインストールが完了します。

インストールされたプログラムは、「APP -」の下に表示されます。

minpathの使用

minpathは、無向グラフの隣接行列表現と隣接表表現の両方をサポートし、.matファイル、テキストファイル、Excelファイルに格納されたデータの読み込みと、手動でのデータ入力をサポートしています。テキストファイルとエクセルファイルには、テーブルヘッダを追加するオプションがあります。

次の動作図は、minpathの動作例です。testdataフォルダーに様々な形式のテストデータが用意されています。

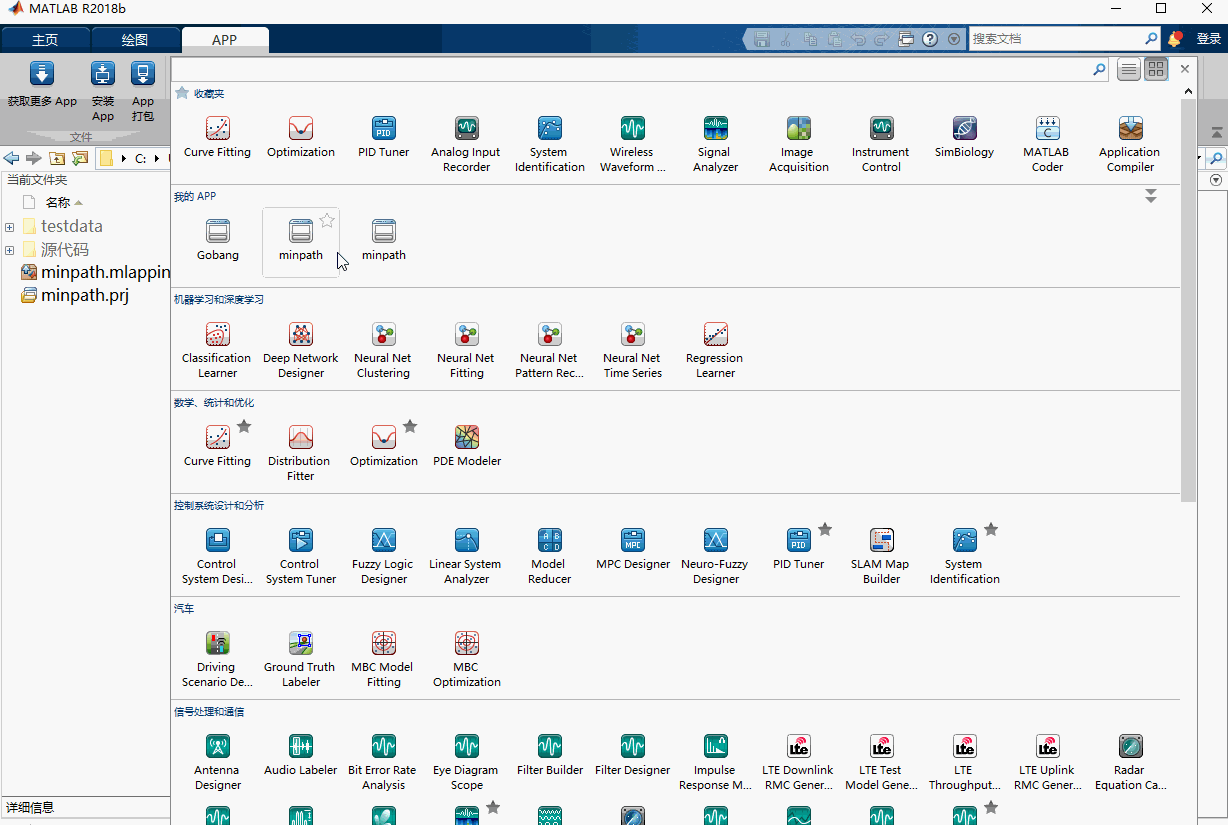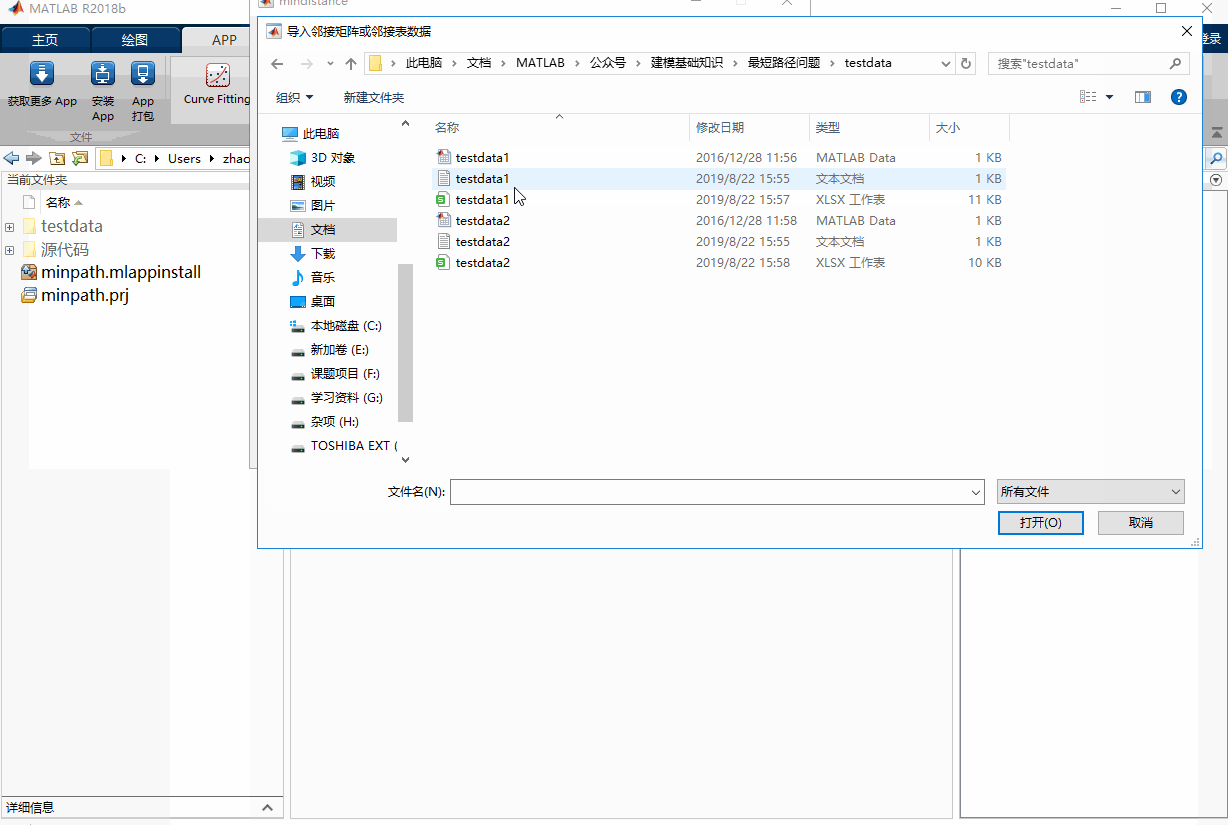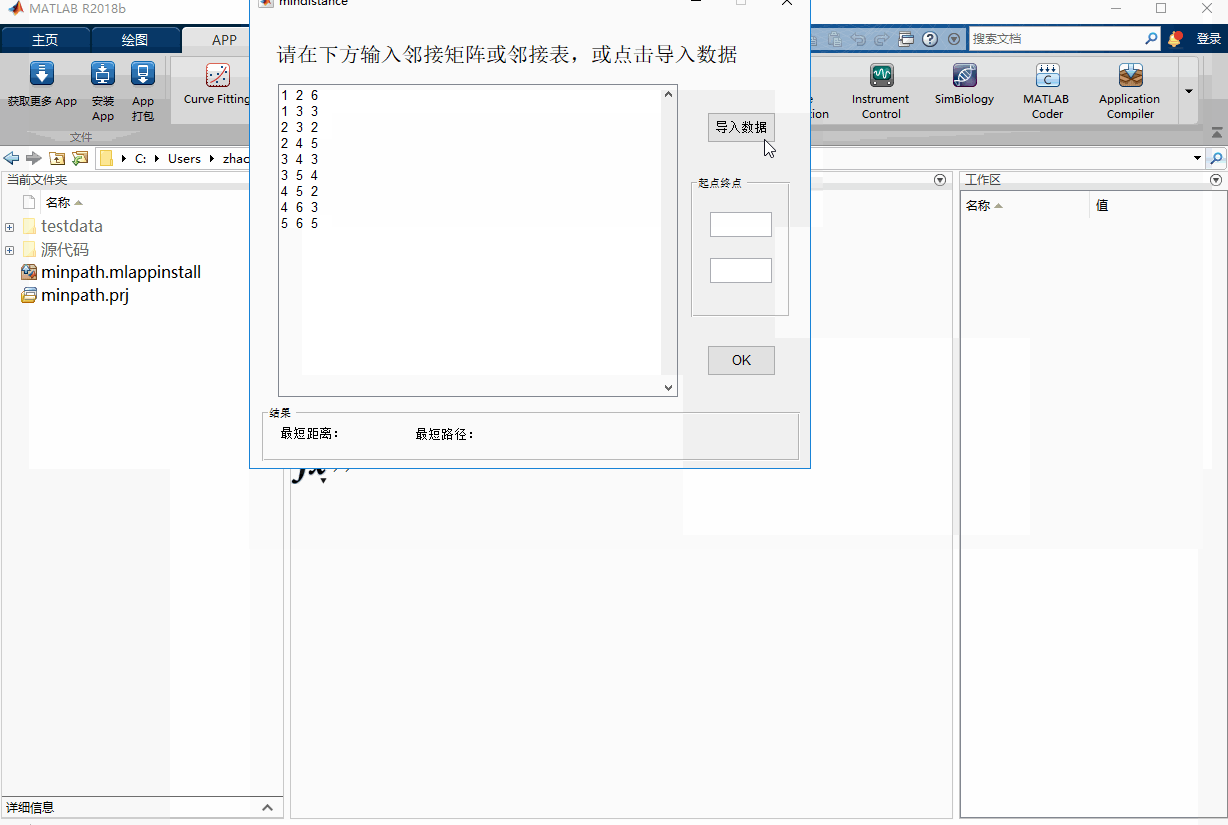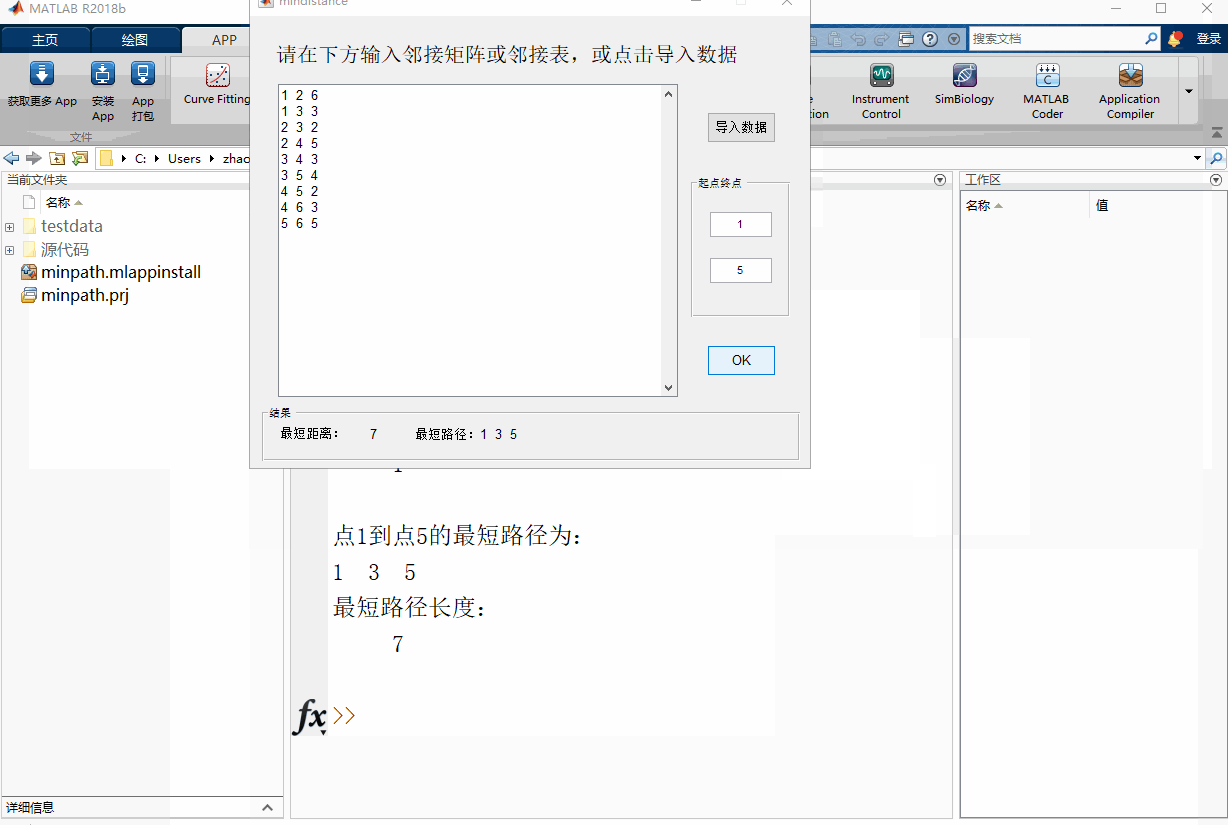
ソースコードの入手や詳細については、公開されているウェブサイトをご参照ください。数理モデリングギルド