[解決済み] Matlabによる最急降下法の実装

質問

Matlabを使って最急降下法を実装し、2変数の関数でテストする必要があります。以下は私がこれまでに行ったことです．

x_0 = [0;1.5]; %Initial guess
alpha = 1.5; %Step size
iteration_max = 10000;
tolerance = 10e-10;

% Two anonymous function to compute 1st and 2nd entry of gradient
f = @(x,y) (cos(y) * exp(-(x-pi)^2 - (y-pi)^2) * (sin(x) - 2*cos(x)*(pi-x)));
g = @(x,y) (cos(x) * exp(-(x-pi)^2 - (y-pi)^2) * (sin(y) - 2*cos(y)*(pi-y)));

%Initiliazation
iter = 0;
grad = [1; 1]; %Gradient

while (norm(grad,2) >= tolerance)
    grad(1,1) = f(x_0(1), x_0(2));
    grad(2,1) = g(x_0(1), x_0(2));
    x_new = x_0 - alpha * grad; %New solution
    x_0 = x_new %Update old solution
    iter = iter + 1;

    if iter > iter_max
        break
    end
end

問題は、例えばWolframAlphaの結果と比べて、同じ値が得られないことです。この関数では、(3.14,3.14) か (1.3,1.3) のどちらかが得られるはずですが、 (0.03, 1.4) が得られています。

どのように解決するのですか？

この方法は局所探索であるため、初期推測とステップサイズによって局所最小に留まる可能性があることを知っておく必要があります。

• 初期推測が異なれば、異なるローカルミニマムを見つけることができます。

• ステップサイズが大きいとアルゴリズムが収束しないので、ステップサイズは重要です。 ステップサイズが小さいと、アルゴリズムが非常に遅くなる。このため、関数の値が小さくなるにつれて、ステップの大きさを調整する必要があります。

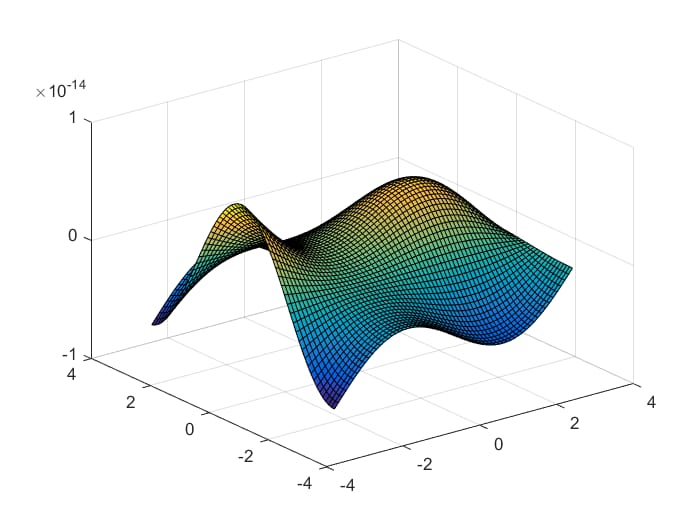
最適化したい関数をプロットして理解することは、常に良いアイデアです（可能であれば）。今回扱う関数は次のようなものです（範囲は [-pi pi] ):

を以下のパラメータ値で設定すると、探しているローカルミニマムに到達します。

x_0 = [2;2]; %Initial guess
alpha = 0.5; %Step size