[解決済み] ランダムはほとんどランダムではない？

問題の最初の部分は、乱数生成器の公開された値を、より小さい数に変換しているため、可能な値の空間が減少していることです。 いくつかの 擬似乱数ジェネレータ の中には、期間中に値を繰り返さないものもありますが、この変換により、領域がはるかに小さいものに変わります。 ドメインが小さくなると、「繰り返さない」という条件が無効になるため、繰り返しの可能性がかなり高くなります。

のようないくつかのアルゴリズムは 線形合同PRNG ( A'=AX|M ) する は、全期間にわたって一意性を保証します。 LCGでは、生成された値はアキュムレータの全状態を含み、追加の状態は保持されません。 ジェネレータは決定論的で、期間内に数を繰り返すことはできません。任意のアキュムレータ値は、1つだけ可能な連続値を意味します。 したがって、各値はジェネレータの期間内に 1 回しか発生しません。 しかし、このようなPRNGの周期は比較的小さく、LCGアルゴリズムの典型的な実装では約2^30であり、異なる値の数より大きくなることはあり得ません。

すべてのPRNGアルゴリズムがこの特性を共有しているわけではなく、あるものは期間内に与えられた値を繰り返すことができます。 OPの問題では メルセンヌ・ツイスター アルゴリズム（Pythonの ランダム モジュール) は非常に長い周期を持っています - 2^32 よりもはるかに大きいです。 線形合同 PRNG とは異なり、アキュムレータが追加の状態を含んでいるので、結果は純粋に前の出力値の関数ではありません。 32ビット整数の出力と ~2^19937 の周期では、そのような保証を提供することは不可能です。

メルセンヌ・ツイスターは、良い統計的、幾何学的特性と非常に長い周期を持つので、PRNGのための一般的なアルゴリズムです-シミュレーションモデルで使用されるPRNGにとって望ましい特性です。

• 良い 統計的特性 は、アルゴリズムによって生成された数字が均等に分布しており、他よりも有意に高い確率で出現する数字がないことを意味します。 統計的特性が悪いと、結果に不要な歪みが生じる可能性があります。

• 良い 幾何学的特性 とは、N個の数の集合がN次元空間の超平面上に存在しないことを意味します。 悪い幾何学的特性は、シミュレーション モデルで偽の相関関係を生成し、結果を歪める可能性があります。

• 長い周期は、シーケンスが最初に戻る前に多くの数を生成できることを意味します。 モデルが多数の反復を必要とする場合、またはいくつかの種から実行する必要がある場合、典型的な LCG 実装から得られる 2^30 ほどの離散数では十分でない場合があります。 MT19337アルゴリズムは、2^19337-1、つまり約10^5821という非常に長い周期を持っています。 それに比べて、宇宙の原子の総数は約10^80と推定されています。

MT19337 PRNGによって生成される32ビット整数は、そのような大きな期間中に繰り返されないように十分な離散値を表すことができない可能性があります。 この場合、重複した値が発生する可能性が高く、十分に大きなサンプルで避けられません。

誕生日のパラドックス」の概要

この問題は、本来、部屋にいる二人が同じ誕生日を持つ確率として定義されます。 重要なポイントは 任意の二人 は誕生日を共有する可能性があります。 人々はこの問題を、部屋の中の誰かが特定の個人と誕生日を共有する確率だと素朴に誤解しがちですが、これが元凶となって 認知バイアス これが、しばしば人々が確率を過小評価する原因となるの原因です。 これは間違った仮定です。特定の個人と一致するという要件はなく、任意の 2 人の個人が一致する可能性があります。

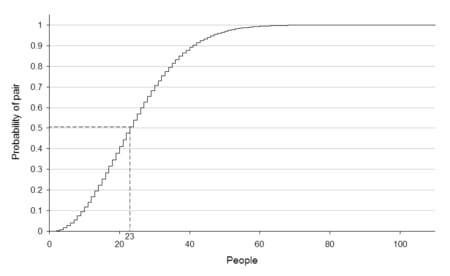
特定の日付に一致する必要がないため、任意の 2 人の間で一致が発生する確率は、特定の個人に一致する確率よりもはるかに高くなります。 むしろ、同じ誕生日を持つ2人の個人を見つければよいのです。 このグラフ (このテーマに関する Wikipedia のページにあります) から、この方法で一致する 2 人を見つける確率が 50% であるためには、部屋の中に 23 人いればよいことがわかります。

から ウィキペディアのこのテーマに関する項目 を得ることができます。 素敵な要約 OPの問題では、365人ではなく、4,500人の「誕生日」の可能性があります。 生成された任意の数のランダムな値 (「人」に相当) に対して、以下の確率を知りたいと思います。 任意の 2 つの同じ値がシーケンス内に現れる確率を知りたいのです。

誕生日のパラドックス」がOPの問題に与えるであろう影響を計算すること

100個の数字の列に対して のペアがあります（参照 問題を理解する ) がマッチする可能性があるため (つまり、1 番目が 2 番目、3 番目などとマッチする可能性があり、2 番目が 3 番目、4 番目などとマッチする可能性がある、など)、その数だけ の組み合わせ の数は 100 を超えています。

から 確率の計算 の式が得られます。 . 以下のPythonコードのスニペットは、マッチングペアが発生する確率を素朴に評価するものです。

# === birthday.py ===========================================
#
from math import log10, factorial

PV=4500          # Number of possible values
SS=100           # Sample size

# These intermediate results are exceedingly large numbers;
# Python automatically starts using bignums behind the scenes.
#
numerator = factorial (PV)          
denominator = (PV ** SS) * factorial (PV - SS)

# Now we need to get from bignums to floats without intermediate
# values too large to cast into a double.  Taking the logs and 
# subtracting them is equivalent to division.
#  
log_prob_no_pair = log10 (numerator) - log10 (denominator)

# We've just calculated the log of the probability that *NO*
# two matching pairs occur in the sample.  The probability
# of at least one collision is 1.0 - the probability that no 
# matching pairs exist.
#
print 1.0 - (10 ** log_prob_no_pair)

この結果、見栄えのする p=0.669 4500の可能な値の母集団からサンプリングされた100の数字内で発生する一致のために。(多分、誰かがこれを検証して、間違っていたらコメントを投稿してくれるでしょう)。 このことから、OPによって観察されたマッチング番号間のランの長さは非常に合理的であるように見えることがわかります。

脚注: シャッフリングを使用して、一意の擬似乱数列を取得する

参照 S.マークからの回答はこちら を参照してください。 この投稿者が言及した手法は、数字の配列（あなたが提供するものなので、ユニークにすることができます）を取り、ランダムな順序にシャッフルします。 シャッフルされた配列から順番に数字を引くと、繰り返さないことが保証された擬似乱数の列が得られます。

脚注：暗号化された安全なPRNG

MTアルゴリズムは 暗号的に安全です。 というのも、数列を観察することで生成器の内部状態を推測することが比較的容易であるからです。 他のアルゴリズムとして ブルーム・ブルーム・シャブ のような他のアルゴリズムは暗号アプリケーションに使われますが、シミュレーションや一般的な乱数アプリケーションには不向きかもしれません。 暗号学的に安全な PRNG は高価であったり（おそらくビグナム計算が必要）、幾何学的な性質が良くない場合があります。 この種のアルゴリズムの場合、一連の値を観測することによって生成器の内部状態を推測することが計算上不可能であることが第一の要件となります。