[解決済み] 前足はどうしたらいいの？

質問

で の中で、私は素晴らしい答えを得ました。 で、前足がプレッシャープレートに当たった場所を検出するのに役立ちました。しかし今、これらの結果を対応する前足にリンクさせるのに苦労しています。

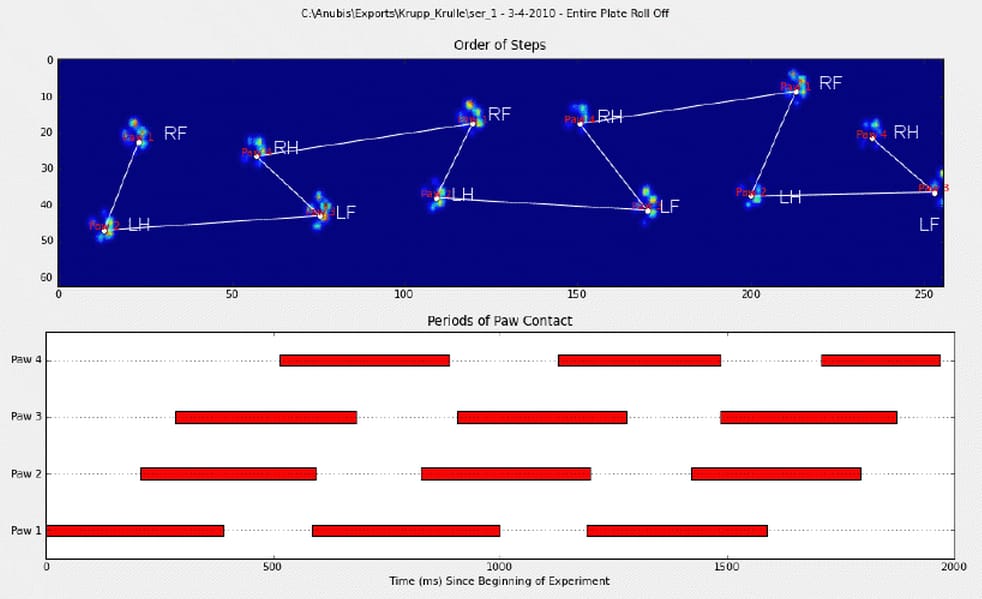
前足に手動でアノテーションをつけました（RF=右前、RH=右後、LF=左前、LH=左後）。

ご覧のように、明らかに繰り返しのパターンがあり、それはほとんどすべての測定で再現されます。 手動で注釈をつけた6つの試行のプレゼンテーションへのリンクです。

最初に考えたのは、ヒューリスティックを使ってソートをする、というようなことでした。

• 前足と後足の間の体重負荷の比率は 60 ～ 40% です。
• 後肢は一般に表面積が小さい。
• 前足は左右に空間的に分かれている（ことが多い）。

しかし、私のヒューリスティックは、思いもよらないバリエーションに遭遇するとすぐに失敗してしまうので、少し懐疑的です。また、おそらく独自のルールを持っている、足の不自由な犬からの測定には対応できないでしょう。

さらに、Joeが提案した注釈は、時々めちゃくちゃになり、前足が実際にどのように見えるかを考慮しません。

いただいた回答から という私の質問に対する回答から、肉球内のピーク検出について の回答から、前足を分類するためのより高度なソリューションがあるのではと期待しています。特に、圧力分布とその進行が肉球ごとに異なるので、まるで指紋のようなんです。これを利用して、単に発生順に並べるだけでなく、前足をクラスター化できるような方法があればいいなと思います。

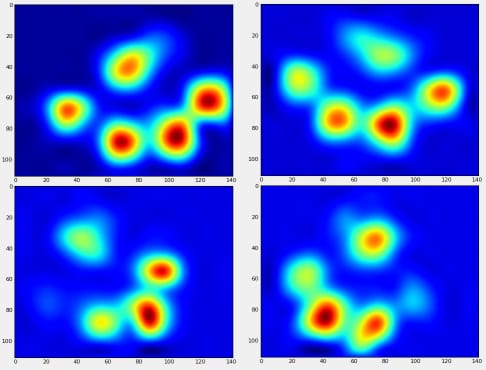
そこで、結果を対応する前足でソートするためのより良い方法を探しています。

挑戦してくれる人のために 辞書を漬けてみた と 各足の圧力データを含むすべてのスライスされた配列は (測定値ごとに束ねられた) と その位置を表すスライス (プレート上の位置と時間的な位置)を表すスライスです。

walk_sliced_data は、測定値の名前である ['ser_3', 'ser_2', 'sel_1', 'sel_2', 'ser_1', 'sel_3'] を含むディクショナリである。各測定値には、抽出された影響を表す別の辞書、[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10] (例: 'sel_1') が含まれています。

また、前足が部分的に（空間的または時間的に）測定されるような「偽の」影響は、無視できることに注意してください。これらは、パターンを認識するのに役立つので有用ですが、分析されません。 分析されることはありません。

そして、興味のある人のために プロジェクトに関する最新情報をブログで公開していますよ。

どのように解決するのですか？

よしっ! 私は最終的に一貫して動作する何かを得ることに成功した! この問題は、数日間私を引っ張った... 楽しいものです。この回答が長くて申し訳ありませんが、いくつかのことについて少し詳しく説明する必要があります... (とはいえ、これまでで最も長い非スパムのstackoverflow回答の記録を打ち立てるかもしれません!)

余談ですが、私は Ivo の完全なデータセットを使用しています。 がリンクを提供してくれた の中で 元の質問 . これは一連のrarファイル（犬一匹につき一個）で、それぞれいくつかの異なる実験がAscii配列として格納されています。この質問にスタンドアロンのコード例をコピーペーストしようとするよりも、ここで bitbucket mercurialリポジトリ にある、完全なスタンドアロンコードです。でクローンすることができます。

hg clone https://[email protected]/joferkington/paw-analysis

---

概要

質問でご指摘のように、この問題には基本的に2つのアプローチ方法があります。実際に両方を使い分けてみます。

1. 前足の衝撃の (時間的および空間的) 順序を使用して、どの前足がどの足であるかを判断する。
2. 純粋にその形状に基づいて、quot;pawprint" を識別しようとする。

基本的に、最初の方法は、犬の足が上記の Ivo の質問で示された台形のようなパターンに従っているときは動作しますが、足がそのパターンに従っていないときはいつでも失敗します。うまくいかないことをプログラムで検出するのはかなり簡単です。

したがって、どの前足がどれであるかを認識するために、それが機能した測定値を使用して、トレーニング データセット (~30 種類の犬からの ~2000 の前足の衝撃) を構築することができ、問題は教師あり分類に減少します (いくつかの追加しわ寄せがありますが...)。画像認識は、通常の教師あり分類の問題よりも少し難しいのです。）

---

パターン解析

最初の方法を詳しく説明すると、犬が普通に歩いているとき（走っていない犬もいるかもしれませんが）、前足は次のような順番で衝撃を与えると予想されます。左前方、右後方、右前方、左後方、左前方......。このパターンは、左前足または右前足のどちらから始めてもかまいません。

これが常にそうである場合、最初の接触時間によって衝撃を単純に並べ替え、前足によってグループ化するためにモジュロ 4 を使用することができます。

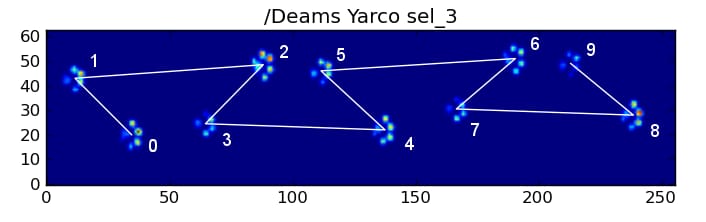
しかし、すべてが "normal"であっても、これはうまくいきません。 これは、パターンの形が台形に似ているためです。後足は、前の前足の後ろに空間的に落ちます。

したがって、最初の前足の衝撃の後の後足の衝撃は、センサープレートから落ちてしまい、記録されないことが多いのです。 同様に、最後の肉球の衝撃は、その前の肉球の衝撃がセンサープレートから外れて記録されなかったため、一連の流れの中で次の肉球でないことがよくあります。

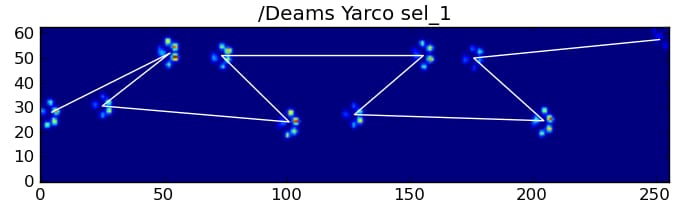
それでも、肉球の衝撃パターンの形状から、これがいつ起こったのか、前足の左右どちらから始めたのかを判断することができます。 (実は、ここでは最後の衝撃の問題は無視しています。)。追加するのはそれほど難しくないのですが)。

def group_paws(data_slices, time):   
    # Sort slices by initial contact time
    data_slices.sort(key=lambda s: s[-1].start)

    # Get the centroid for each paw impact...
    paw_coords = []
    for x,y,z in data_slices:
        paw_coords.append([(item.stop + item.start) / 2.0 for item in (x,y)])
    paw_coords = np.array(paw_coords)

    # Make a vector between each sucessive impact...
    dx, dy = np.diff(paw_coords, axis=0).T

    #-- Group paws -------------------------------------------
    paw_code = {0:'LF', 1:'RH', 2:'RF', 3:'LH'}
    paw_number = np.arange(len(paw_coords))

    # Did we miss the hind paw impact after the first 
    # front paw impact? If so, first dx will be positive...
    if dx[0] > 0: 
        paw_number[1:] += 1

    # Are we starting with the left or right front paw...
    # We assume we're starting with the left, and check dy[0].
    # If dy[0] > 0 (i.e. the next paw impacts to the left), then
    # it's actually the right front paw, instead of the left.
    if dy[0] > 0: # Right front paw impact...
        paw_number += 2

    # Now we can determine the paw with a simple modulo 4..
    paw_codes = paw_number % 4
    paw_labels = [paw_code[code] for code in paw_codes]

    return paw_labels

これだけのことをしても、正しく動作しないことがよくあります。完全なデータセット内の多くの犬は走っているように見え、前足の衝撃は犬が歩いているときと同じ時間順序に従わない。(あるいは、その犬は重度の股関節の問題を抱えているだけかもしれませんが...)

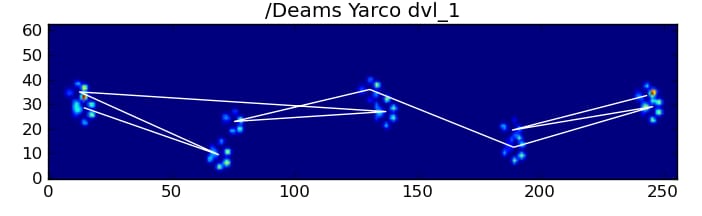
幸いなことに、前足の衝撃が私たちが期待する空間パターンに従っているかどうかをプログラムで検出することができます。

def paw_pattern_problems(paw_labels, dx, dy):
    """Check whether or not the label sequence "paw_labels" conforms to our
    expected spatial pattern of paw impacts. "paw_labels" should be a sequence
    of the strings: "LH", "RH", "LF", "RF" corresponding to the different paws"""
    # Check for problems... (This could be written a _lot_ more cleanly...)
    problems = False
    last = paw_labels[0]
    for paw, dy, dx in zip(paw_labels[1:], dy, dx):
        # Going from a left paw to a right, dy should be negative
        if last.startswith('L') and paw.startswith('R') and (dy > 0):
            problems = True
            break
        # Going from a right paw to a left, dy should be positive
        if last.startswith('R') and paw.startswith('L') and (dy < 0):
            problems = True
            break
        # Going from a front paw to a hind paw, dx should be negative
        if last.endswith('F') and paw.endswith('H') and (dx > 0):
            problems = True
            break
        # Going from a hind paw to a front paw, dx should be positive
        if last.endswith('H') and paw.endswith('F') and (dx < 0):
            problems = True
            break
        last = paw
    return problems

したがって、単純な空間分類が常に機能するわけではありませんが、機能する場合はそれなりの信頼性を持って判断することができます。

トレーニングデータセット

正しく動作したパターンベースの分類から、正しく分類された前足の非常に大きなトレーニングデータセットを構築することができます（32種類の犬から約2400個の前足が衝突！）。

これで、左前足などの平均的な前足がどのように見えるかを調べ始めることができます。

これを行うには、どの犬でも同じ次元である、ある種の「肉球メトリック」が必要です。(完全なデータセットでは、非常に大きな犬と非常に小さな犬の両方があります!) アイリッシュ エルクハウンドの足跡は、トイ プードルの足跡よりもはるかに広く、非常に重くなります。 そこで、それぞれの足跡を再スケーリングして、a)ピクセル数が同じになるように、b)圧力値が標準化されるようにする必要があります。 これを行うために、各足跡を 20x20 のグリッドに再サンプリングし、足跡の衝撃の最大、最小、および平均圧力値に基づいて圧力値を再スケーリングしました。

def paw_image(paw):
    from scipy.ndimage import map_coordinates
    ny, nx = paw.shape

    # Trim off any "blank" edges around the paw...
    mask = paw > 0.01 * paw.max()
    y, x = np.mgrid[:ny, :nx]
    ymin, ymax = y[mask].min(), y[mask].max()
    xmin, xmax = x[mask].min(), x[mask].max()

    # Make a 20x20 grid to resample the paw pressure values onto
    numx, numy = 20, 20
    xi = np.linspace(xmin, xmax, numx)
    yi = np.linspace(ymin, ymax, numy)
    xi, yi = np.meshgrid(xi, yi)  

    # Resample the values onto the 20x20 grid
    coords = np.vstack([yi.flatten(), xi.flatten()])
    zi = map_coordinates(paw, coords)
    zi = zi.reshape((numy, numx))

    # Rescale the pressure values
    zi -= zi.min()
    zi /= zi.max()
    zi -= zi.mean() #<- Helps distinguish front from hind paws...
    return zi

この後、左前足、右後足などの平均的な足がどのようなものか、ようやく見てみることができます。 これは30匹の犬の大きさを平均したものですが、一貫した結果が得られているようです。

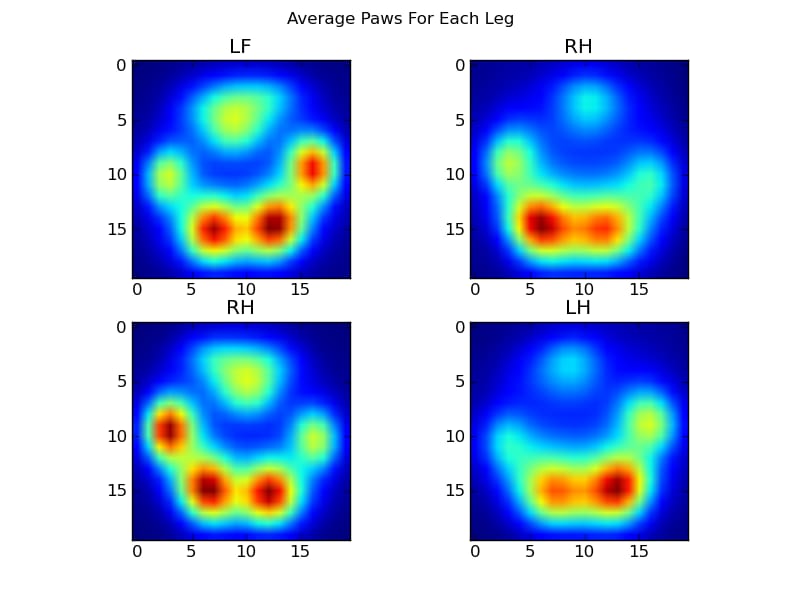
しかし、これらについて分析を行う前に、平均値（全犬種の全脚の平均的な前足）を差し引く必要があります。

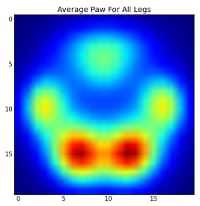
今度は、もう少しわかりやすい平均値からの差を分析します。

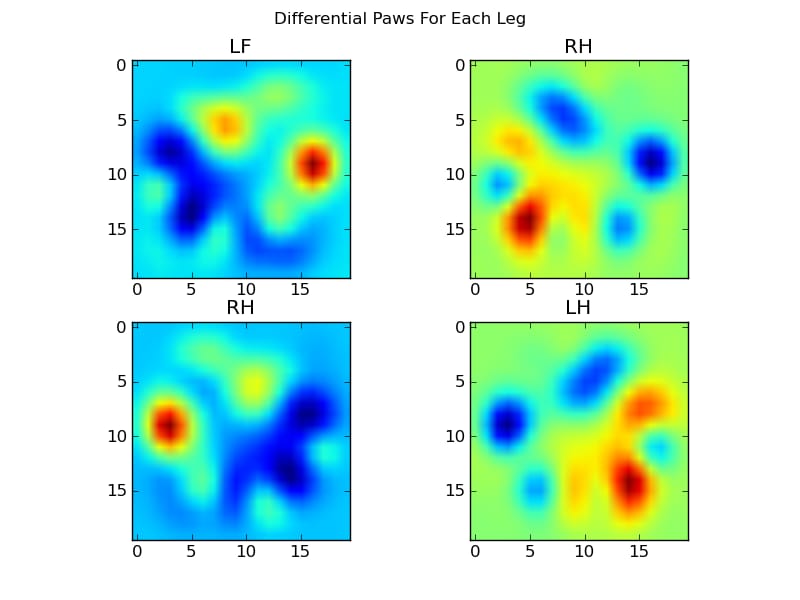
画像による肉球の認識

OK... ついに、前足を照合するためのパターンのセットができました。 各足は 400 次元のベクトルとして扱うことができます ( paw_image 関数で返される) 400次元ベクトルとして扱うことができ、この4つの400次元ベクトルと比較することができる。

残念ながら、通常の教師あり分類アルゴリズム (つまり、単純な距離を使用して、4 つのパターンのうちどれが特定の足跡に最も近いかを見つける) を使用するだけでは、一貫して機能しません。実際、トレーニング データセットでは、ランダムな偶然よりはるかに良い結果を得ることはできません。

これは画像認識における一般的な問題です。入力データの次元が高く、画像の性質がややファジーであるため (つまり、隣接するピクセルには高い共分散がある)、テンプレート画像からの画像の差を見るだけでは、それらの形状の類似性のあまり良い指標を得ることができません。

固有ポーズ

これを回避するには、quot;固有脚のセット (顔認識におけるquot;固有顔と同じ) を構築し、各足跡をこれらの固有脚の組み合わせとして記述する必要があります。 これは主成分分析と同じで、基本的にデータの次元を減らす方法を提供し、距離が形状の良い尺度になるようにします。

次元よりも多くの学習画像があるため(400に対して2400)、速度のための派手な線形代数を行う必要はありません。訓練データセットの共分散行列で直接作業することができます。

def make_eigenpaws(paw_data):
    """Creates a set of eigenpaws based on paw_data.
    paw_data is a numdata by numdimensions matrix of all of the observations."""
    average_paw = paw_data.mean(axis=0)
    paw_data -= average_paw

    # Determine the eigenvectors of the covariance matrix of the data
    cov = np.cov(paw_data.T)
    eigvals, eigvecs = np.linalg.eig(cov)

    # Sort the eigenvectors by ascending eigenvalue (largest is last)
    eig_idx = np.argsort(eigvals)
    sorted_eigvecs = eigvecs[:,eig_idx]
    sorted_eigvals = eigvals[:,eig_idx]

    # Now choose a cutoff number of eigenvectors to use 
    # (50 seems to work well, but it's arbirtrary...
    num_basis_vecs = 50
    basis_vecs = sorted_eigvecs[:,-num_basis_vecs:]

    return basis_vecs

これらは basis_vecs が固有値となります。

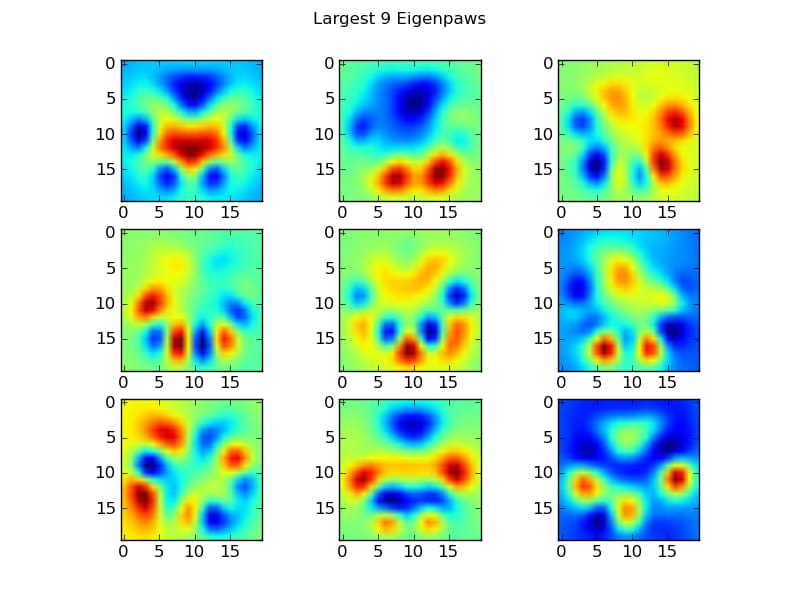
これらを使うには、各足画像（20×20の画像ではなく、400次元のベクトルとして）を基底ベクトルに単純にドット（つまり行列の掛け算）します。これにより、50次元のベクトル（基底ベクトルあたり1要素）が得られ、これを用いて画像を分類することができます。20×20の画像と20×20のテンプレート肉球を比較するのではなく、50次元に変換した画像と50次元に変換したテンプレート肉球をそれぞれ比較するのです。 これは、各足の指がどのように配置されているかなどの正確な小さなばらつきに対する感度がはるかに低く、基本的に問題の次元を関連する次元だけに減らすことができます。

固有表現に基づく肉球の分類

あとは、50次元のベクトルと各脚のquot;template"ベクトルとの距離を使って、どの肉球がどの肉球かを分類すればよいのです。

codebook = np.load('codebook.npy') # Template vectors for each paw
average_paw = np.load('average_paw.npy')
basis_stds = np.load('basis_stds.npy') # Needed to "whiten" the dataset...
basis_vecs = np.load('basis_vecs.npy')
paw_code = {0:'LF', 1:'RH', 2:'RF', 3:'LH'}
def classify(paw):
    paw = paw.flatten()
    paw -= average_paw
    scores = paw.dot(basis_vecs) / basis_stds
    diff = codebook - scores
    diff *= diff
    diff = np.sqrt(diff.sum(axis=1))
    return paw_code[diff.argmin()]

以下は、その結果の一部です。

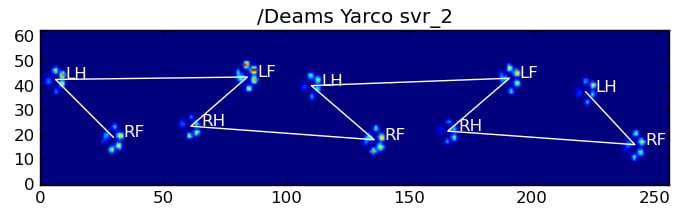
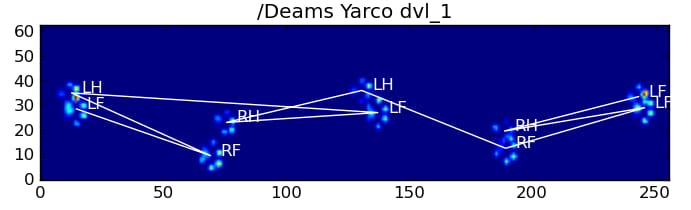
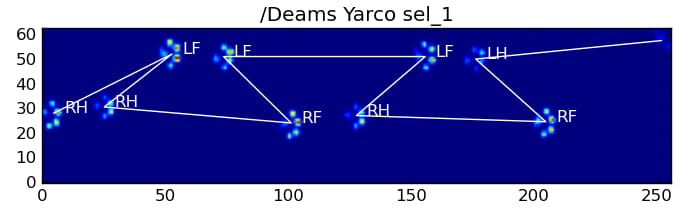
残された問題点

特に、小型犬で足跡がはっきりつかない...という問題があります(大型犬では、センサーの解像度で足先がはっきり分かれているため、最も効果的です。)。また、台形パターン方式では認識できた部分的な肉球が、この方式では認識できないこともあります。

しかし、固有肉球解析は本質的に距離メトリックを使用するので、両方の方法で足を分類し、固有肉球解析のコードブックからの最小距離がある閾値以上になったときに台形パターンベースのシステムにフォールバックすることができます。まだ実装していませんが。

ふぅ...。長かった! こんな楽しい質問をしてくれるIvoさんに脱帽です。