[解決済み】数独の正方形の凸凹の欠点を取り除くには？

質問

私は楽しいプロジェクトをやっていました。OpenCVを使用して入力画像から数独を解く（Googleゴーグルなどのように）。そして、私はタスクを完了しましたが、最後に私はここに来るために小さな問題を見つけました。

プログラミングはOpenCV 2.3.1のPython APIを使って行いました。

以下は、私が行ったことです。

1. 画像を読み込む
2. 輪郭を見つける
3. 面積が最大となるものを選ぶ（正方形に多少相当する）。

4. 角の点を探す。

   例）以下のようになります。

   

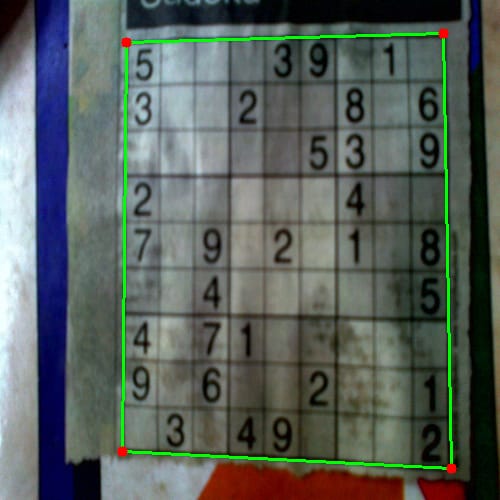
   ( 緑色の線が数独の真の境界線と正しく一致しているため、数独は正しくワープすることができます。 . 次の画像をチェック)

5. 画像を正方形にワープさせる

   をイメージしてください。

   

6. OCRを実行する（このために、私は以下の方法を使用しました。 OpenCV-Pythonで作る簡単な数字認識OCR )

そして、その方法はうまくいった。

問題あり。

チェックアウト この画像は

この画像に手順4を実行すると、以下のような結果になります。

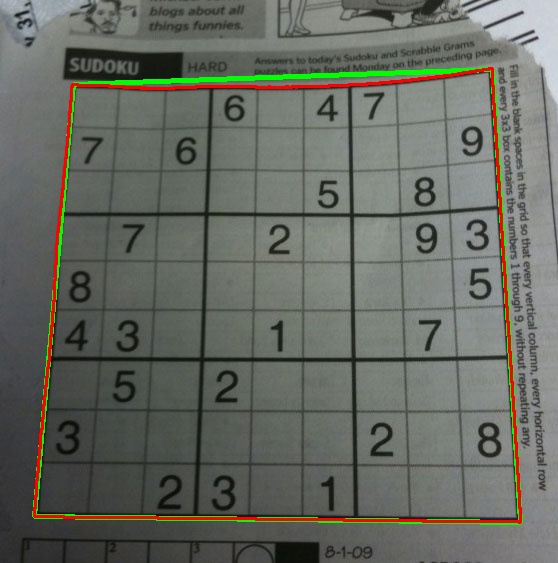
赤い線が本来の輪郭で、これが数珠つなぎになる。

緑色の線は、歪んだ画像の輪郭を近似したものです。

もちろん、数独の上端では緑色の線と赤色の線の間に違いがあります。そのため、ワープしている間、数独の本来の境界線を得ることができません。

私の質問:

数独の正しい境界線、つまり赤い線の上で画像をワープさせるには、あるいは赤い線と緑の線の差を取り除くにはどうしたらよいでしょうか？OpenCVにこのためのメソッドはありますか？

どのように解決するのですか？

私はうまくいく解決策を持っていますが、あなた自身でOpenCVに翻訳する必要があります。これは Mathematica で書かれています。

まず、画像の明るさを調整するために、各ピクセルをクロージング演算の結果で分割します。

src = ColorConvert[Import["http://davemark.com/images/sudoku.jpg"], "Grayscale"];
white = Closing[src, DiskMatrix[5]];
srcAdjusted = Image[ImageData[src]/ImageData[white]]

<イグ

次に、背景を無視（マスク）するために、数独の領域を見つけることです。そのために、連結成分分析を使って、最も大きな凸の面積を持つ成分を選択します。

components = 
  ComponentMeasurements[
    ColorNegate@Binarize[srcAdjusted], {"ConvexArea", "Mask"}][[All, 
    2]];
largestComponent = Image[SortBy[components, First][[-1, 2]]]

<イグ

この画像を塗りつぶすことで、数独のグリッドのマスクを得ることができる。

mask = FillingTransform[largestComponent]

<イグ

さて、2次微分フィルタを使って、2枚の画像から縦線と横線を見つけることができる。

lY = ImageMultiply[MorphologicalBinarize[GaussianFilter[srcAdjusted, 3, {2, 0}], {0.02, 0.05}], mask];
lX = ImageMultiply[MorphologicalBinarize[GaussianFilter[srcAdjusted, 3, {0, 2}], {0.02, 0.05}], mask];

<イグ

この画像から再び連結成分分析を使ってグリッド線を抽出します。グリッド線は桁よりもずっと長いので、ノギス長を使ってグリッド線に接続された成分のみを選択することができます。これを位置でソートすると、画像内の縦・横のグリッド線ごとに2x10のマスク画像が得られます。

verticalGridLineMasks = 
  SortBy[ComponentMeasurements[
      lX, {"CaliperLength", "Centroid", "Mask"}, # > 100 &][[All, 
      2]], #[[2, 1]] &][[All, 3]];
horizontalGridLineMasks = 
  SortBy[ComponentMeasurements[
      lY, {"CaliperLength", "Centroid", "Mask"}, # > 100 &][[All, 
      2]], #[[2, 2]] &][[All, 3]];

<イグ

次に、縦と横の格子線のペアをそれぞれ取り出して拡張し、ピクセルごとに交点を計算し、結果の中心を計算します。これらの点がグリッド線の交点となる。

centerOfGravity[l_] := 
 ComponentMeasurements[Image[l], "Centroid"][[1, 2]]
gridCenters = 
  Table[centerOfGravity[
    ImageData[Dilation[Image[h], DiskMatrix[2]]]*
     ImageData[Dilation[Image[v], DiskMatrix[2]]]], {h, 
    horizontalGridLineMasks}, {v, verticalGridLineMasks}];

<イグ

最後に、これらの点を通るX/Yマッピングのための2つの補間関数を定義し、これらの関数を用いて画像を変換する。

fnX = ListInterpolation[gridCenters[[All, All, 1]]];
fnY = ListInterpolation[gridCenters[[All, All, 2]]];
transformed = 
 ImageTransformation[
  srcAdjusted, {fnX @@ Reverse[#], fnY @@ Reverse[#]} &, {9*50, 9*50},
   PlotRange -> {{1, 10}, {1, 10}}, DataRange -> Full]

<イグ

どれも基本的な画像処理機能なので、OpenCVでも可能なはずです。スプラインベースの画像変換は難しいかもしれませんが、本当に必要とは思えません。おそらく、今使っている透視変換を個々のセルに対して使えば、十分な結果が得られると思います。