分類アルゴリズムにおける精度の問題点

統計学では、同様の行列（0：偽、1：真）があり、FP：偽（悪人を逃がす）、FNは真（善人を誤って殺す）として捨てられ、悪人が多く逃がす（確率が高い）、つまり、"law"が厳しくないので善人が少なく誤って殺される（確率が低い）はずである。(考えてみれば、quot;law"判定のもとでは、悪人が釈放されれば、善人も釈放されなければならず、誤って殺されることはないのです）。同様に、FNが小さければ、釈放される悪人が少なく（確率が低い）、"lawが厳しければ、誤って殺される善人が多く（確率が高い）、FPが大きくなる。

まとめると FPとFNは負の相関があり、すなわちFPが増加するとFNは減少し、FPが減少するとFNは増加する。

精度＝TP/(FP+TP)

リコール＝TP/(FN+TP)

見ての通り、精度とリコールの分子は同じで、精度の分母は（FP+TP）、リコールの分母は（FN+TP）であり、どちらも分母にTPが含まれているので、精度とリコールの大きさの関係はFPとFNで決まり、FPとFNは負の相関があることがわかります。 つまり、精度が上がるとリコールが減り、精度が下がるとリコールが増えるという負の相関があるのです。

2つの指標に差がある場合、どちらを優先すべきでしょうか？

具体的なシナリオによって異なる

(1) ケース2の患者予測システムのように、本当に病気である人を全て病気であると予測する（＝想起）ことが期待できるので、想起（リコール）をより重視する。

そして精度ですが、病気になると予測される人の数が少なくても問題なく、この時点では病気でない人をより多く病気になると予測しているだけで、せいぜい病気でない人に少しづつ検査を受けてもらっているに過ぎないのです。

(2) ケース4：株価予測システム

株価予測システムでは、一般的に、明日はどの銘柄が上がるか、今日はどの銘柄を買えばいいかを重視する。つまり、1：株価が上がっていることを意味する 0：株価が下がっていることを意味する

上がると予測された銘柄は、実際には上がる（そうでなければ実際には下がるので、今日買って明日下がったらまずいのではないか）（＝精度）と予想されるので、この場合はprecision（精度）をより重視します

そして、リコール（思い出し）ですが、ある銘柄が実際に上がり、その銘柄の株価も上がると予測する確率は比較的小さく（つまり、実際に上がった銘柄で、下がると予測され、買わなかった銘柄も多くありますが、それで大きな損失にはなりません）、精度が高く、買った株が上がっていれば、全て問題なしとリターンに影響を与えません。

(3) 精度と再現率が等しく重要な文脈もあり、両方を考慮したf1_scoreを導入する必要がある

2.2 f1_score

2.2.1 f1_scoreの算出方法

f1_score は、以下の精度および再現率です。 合計平均

f1_score = 2 / [(1/precision) + (1/recall)],

f1_scoreはprecisionとrecallのどちらかが低ければ低く、precisionとrecallの両方が高い場合のみ高くなります。

などです。 f1_score = 0.5 when precision = 0.5, recall = 0.5; (i.e. when precision=recall, f1_score =precision=recall)

f1_score = 0.18 精度 = 0.9 リコール = 0.1 (算術平均を使うと0.5となり、リコールの方が低いという事実がうまく反映されない)

精度=1.0、再現率=0の場合、f1_scoreは無意味であり、プログラムは0にします（一方、算術平均を使用した場合、再現率が0であるという事実をうまく反映していないため0.5）。

2.2.2 f1_scoreのプログラムによる実装

詳細はプログラムをご覧ください f1_score.ipynb

3. 精度リコールカーブ

3.1 閾値による精度と想起の調整

あるシナリオでは、precision_scoreを大きくする必要があり、あるケースではrecall_scoreを大きくする必要があり、あるケースでは、両方が必要です。precision_scoreとrecall_scoreを調整するためにはどうしたらよいでしょうか？

閾値を下げると精度が下がり、再現性が上がる。閾値を上げると精度が上がり、再現性が下がる。

3.2 より直感的に見るために、異なる閾値におけるprecision_scoreとrecall_scoreをプログラム的に計算します。また、精度とリコールの大きさは負の相関がある。

ロジスティック回帰では、閾値=0を使用し、閾値を変更することで精度と再現率を調整することができる。利用できるもののうち

sklearn.linear_model.LogisticRegression.decision_function ( サンプルの信頼度スコアを予測する ) 予測結果を得るために適切な閾値を自分で定義してください。

詳しくは、こちらをご覧ください。 precision_score_VS_recall_score.ipynb

3.3 プログラミング、異なるprecision_recall_curveでのプロット

(1) まず、LogisticRegression の decision_function メソッドでスコアを取得し、異なる閾値に基づく分類結果、 confusion_matrix, precision_score, recall_score を取得します。

(2) precision_recall_curveのプロット1

(3) precision_recall_curve2 (PR_curveとも呼ばれる)をプロットする。

詳細はコード参照：precision_recall_curve.ipynb

3.3 PR_curveの解析。

下図に示すように、Bのどの地点でもAより精度、再現率が大きくなっており、BのモデルがAより優れていることがわかる。また、AとBで囲まれた面積でモデルの良し悪しを判断することができ、囲まれた面積が大きいほど、良いモデルであることがわかります。(ただし，一般にモデルの良し悪しはROC曲線で囲まれた領域で判断します( その理由については、4．をご覧ください。 ROC AUC))

4. ROC AUC

曲線下面積（Receiver Operating Characterisitc Area Under Curve）。

<スパンロック <スパンは、特異度( FPR <スパン <スパン垂直方向シッティングマークと感度( TPR <スパン ) について水平縦方向座りマーク曲線の構成ライン (その <スパン実際の <スパンは折りたたまれていますライン ).

<スパン AUC <スパン <スパンはいロック <スパン " <スパンクライン " とのことです。 y = 0 そして x = 1 ストレートラインが形成する面。製品 .

4.1 ROC_curve,TPR,FPRの簡単な紹介

ROC_curve(Receiver Operation Characteristic Curve)の略。 TPR (True positive rate) と FPR (Flase positive rate) の関係を記述する。

(1) TPR

TPRのこと。真が正で、予測も正である確率。

TPR = TP/(TP+FN) = リコール

(2) FPR

FPR：すなわち、真は負だが、予測は正である確率

fpr = fp/(fp+tn)

(3) TPRとFPRの関係

4.2 TPR、FPR、ROC_curveのプログラム実装

TPR_FPR_ROC.ipynb

4.3 ROC_curveの解析

ROC_curve を以下に示す。

ROC_curveはTPR (True positive rate)とFPR (Flase positive rate)の関係を記述したものである。TPRとFPRは偏ったデータに対してあまり敏感ではないので、ROC_curveも偏ったデータに対してあまり敏感ではない。通常、ROC_curveで囲まれた領域を用いて、モデルの良し悪しを判断する。

明らかに、モデルAはモデルBよりも優れています。

PR曲線とROC曲線の違いの核心はTNである。PR曲線は実際にはTNを反映していないことがわかる。したがって、TNが重要でないアプリケーションシナリオがある場合、PR曲線は良い指標となる（実際には、TNを消去することによって極端に偏ったデータの影響を除去し、その結果としてFP、FN、TPを増幅するためにPrecisionとRecallが使用されている）。

ROC曲線はTN、FP、FN、TPを組み合わせたものですが、TNが極端に多い場合、FP、FN、TPの変化には鈍感になります。つまり、TNがそれほど多くない（データがそれほど歪んでいない）場合や、TNが重要な考慮事項となる場合、ROCはPRにないものを反映します（"0"の発生を正しく予測することに関心がある場合、TNが重要な考慮事項となります、例えば株価予測では、上昇のみならず下落も正しく予測する必要があります）。

ps.

機械学習の分野では、メトリクスの場合、多くの場合、誰を選ぶかという問題ではなく、可能であればすべてのメトリクスを見て、学習済みモデルに問題がないかを判断する必要があります。病院でボディチェックを受けるようなもので、最初にどのメトリクスを見るかを決めて、そのメトリクスだけを見るのではなく、可能であればすべてのメトリクスを見るのです。なぜなら、どれかひとつの指標に問題があるということは、体の機能のどれかに問題があるということかもしれないからです。

つまり、目標は単一の「ベストな」指標を見つけることではなく、すべての指標の背後にあるものを理解し、その指標に問題がある場合は、どこに問題があるかを判断して、モデルを改善することなのです。改善の方向性は一つかもしれませんが。例えば、病院に行ったときに、主な症状は発熱で、主な異常指標は体温なので、体温を下げる治療を中心に行いますが、その治療の過程で他の指標を無視するわけではありません。しかし、これは温度を正常なレベルまで下げれば、治療の過程で他の指標を無視してもよいという意味ではありません。冷やそうとする過程で、血圧、心拍数、白血球、赤血球、これらの指標に異常が見つかれば、すぐに対応する必要があるのです。

5. 多階級化問題(MCP)

5.1 注意事項

sklearn の LogisticRegression() は、本質的に (OVR を使用して) 複数分類の問題を解くことができます。

precision_scoreのパラメータaverage = 'マイクロ'

recall_scoreのパラメータ平均='micro'

confusion_matrix は本来、複数分類の問題を解決することができる

5.2 confusion_matrixのプロット

なぜconfusion_matrixを描く必要があるのでしょうか？

confusion_matrixをプロットすることで、色から混同しやすいカテゴリを判断し、そのカテゴリの閾値を調整することで、それに応じてモデルを改善することができます。もちろん、データ自体に問題があるために混乱する場合もあります。

わかりやすい混同行列を以下に示す。

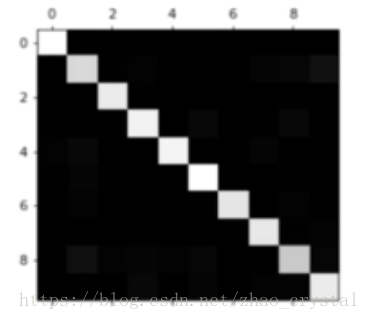
色が明るいほど、その位置の値が大きいことを意味します。見ての通り、対角線上の位置（分類上正しい位置）の値が大きくなっており、当初は分類モデルがかなり優秀であることが分かります。しかし、そうとは言い切れない曖昧な明るい部分もあるので、confusion_matrixを処理することで、見せたい情報を得ることができます。

調整後のconfusion_matrixは次のようになります。

図からわかるように、(1,8)(3,8)と解答を混同しやすいのです。

(1) (1,8)(3,8)分類の閾値を適宜微調整して、分類の精度や再現性を向上させる。

(2) 誤分類がアルゴリズムレベルではなく、データレベルにある可能性があるので、画像1,3,8などを取り出して見て、なぜ誤分類が起きているのかを知覚的に分析することができる。

分類アルゴリズムにおける精度の問題点

1. 混同行列、精度、再現率

1.1 難読化マトリックス、精度、リコールを導入する理由

1.2 confusion_matrix（コンフュージョンマトリックス

1.3 精度と再現性

1.3.1 精度（プレシジョン）。

1.3.2 リコール(recall)。

1.4 confusion_matrix、precision、recallのプログラムによる実装

2. f1_score

2.1 f1_scoreを導入する理由