リリカルスコープ、ダイナミックスコープ、コールバック、クロージャを一挙紹介

前置き

知っているようで明確に理解できていなかった概念を完全網羅しました。内容はwikiのページを参照し、その上で自分なりに理解したことを追加しています。

レキシカルスコープとダイナミックスコープ

言語に関係なく、私たちは常に、グローバル変数、パッケージ変数、モジュール変数、ローカル変数、ローカル変数といった一般的な呼称のような、スコープ（またはライフサイクル）の概念を学びます。これらのスコープがどのように呼ばれるかに関わらず、それを実装する目的は同じである。

(1)名前の衝突を避けるため。

(2) 変数のライフサイクルを修飾する（この記事は変数名で語っており、他の名称もルール上は同じである）。

しかし、言語によってスコープのルールは異なりますが、簡単な基本を学べば十分応用が効きますが、プログラミングの仕様がありますから。(1)名前の衝突を避けるようにする、(2)localに似た修飾語を付けて効果範囲を最小化する、(3)コードブロックを入れる、など。ただ、スコープの効果メカニズムを検証するのは簡単ではない（Pythonを学ぶときは検証に長い時間をかけ、perlを学ぶときは検証に長い時間をかけた）のだが、この記事のレキシカルスコープのルール（Lexical scoping）とダイナミックスコープのルール（動的スコープ）の理解が重要であることは間違いない。 この二つのルールはすべての言語に対してマクロ的に汎用的である。

bashの下での非常にシンプルなコードです。

x=1
function g(){ echo "g: $x" ; x=2; }
function f(){ local x=3 ; g; echo "f: $x"; } # output 2 or 3
f # Output 1 or 3?
echo $x # Output 1 or 2?

bashの場合、上記の出力はそれぞれ3（g関数内のecho）、2（f関数内のecho）、1（最終行のecho）です。しかし、他の言語で同じ意味合いのコードを書くと、違う結果（それぞれ1、3、2、例えばperlはlocalをmyに置き換えます）になることがあります。

これには、すべてのプログラミング言語に共通する、レキシカルスコープ（C言語のスタティックと同様）とダイナミックスコープという2つのスコープの概念が関わっています。レキシカルスコープというのは、「レキシカル」という言葉とは全く関係なく、「テキストセグメントスコープ」とでも呼んだ方がよいでしょう。この2つを区別するには、「関数out_funcにネストされた内部関数in_funcはout_funcの環境を見ることができるか」という質問に答えればよいのです。

上記のbashのコードについて、もしこのコードがすべての言語の疑似コードであったとしたら。

レキシカルスコープ言語の場合、f の実行は g を呼び出します。g は f のテキストセグメント内の変数にアクセスできず、レキシカルスコープでは g は f の一部ではなく、g の定義テキストセグメントがグローバルスコープにあるので f からジャンプアウトしたものとみなされます。関数 g の定義テキスト セグメントが f の内部にある場合、g は f のテキスト セグメントの一部となります。

• ですから、gは、fのテキストセグメントが local x=3 を設定するため、g の echo はグローバル変数 x=1 を設定し、さらに x=2 つまり、全体の処理で出力されるのは 1 3 2

動的スコープを持つ言語では、fの実行はgを呼び出し、gはfのテキスト内の変数にアクセスできる。動的スコープでは、gはfのテキストセグメントの一部であり、f内のネストした関数と見なされる。

• そのためgには local x=3 ということで、g の echo は 3 を出力します。g で x=2 を設定した後、それは f の内側の入れ子関数にのみ設定されるので、x=2 は g のテキストセグメントと f のテキストセグメントの両方から見えますが（g は f の一部なので）、f のテキストセグメントの外側からは見えないので、f の echo は 2、最後の行の echo は 1 と出力されます。 3 2 1

まとめると

• 字句のスコープはコンパイル時に関連付けられ、関数の場合は関数の定義テキストフィールドの位置で決定される。
• 動的スコープはプログラムの実行中に関連付けられ、関数の場合は関数の実行位置がスコープを決定します。

bashは動的なスコープルールを実装しているので。そのため、出力は 3 2 1 . perlの場合、my修飾子はレキシカルスコープルールを実装し、local修飾子はダイナミックスコープルールを実装しています。

例えば、my修飾子を使ったPerlのプログラムです。

#! /usr/bin
$x=1;
sub g { print "g: $x\n"; $x=2; }
sub f { my $x=3; g(); print "f: $x\n"; } # lexical scope
f(); 
print "$x\n"; 

実行結果です。

[fairy@fairy:/perlapp]$ perl scope2.pl
g: 1
f: 3
2

ローカルモディファイアを使用するPerlプログラム。

#! /usr/bin
$x=1;
sub g { print "g: $x\n"; $x=2; }
sub f { local $x=3; g(); print "f: $x\n"; } # dynamic scope
f(); 
print "$x\n"; 

実行結果です。

[fairy@fairy:/perlapp]$ perl scope2.pl
g: 3
f: 2
1

言語によっては、特に最近のものでは、1つのスコープルールしかサポートしていないものもあります。 では $ref_func=\&myfunc もこの関数を指しています。

ある関数を別の関数の引数として受け取ります。例えば、myfuncとfunc1という名前の2つの関数がある場合、以下のようになります。 $ref_func は、func1 を myfunc の引数として取ります。

• この動作は、一般的にmyfunc関数で、何らかのロジックを満たすものに対してfunc1関数を実行するために使用されます。
• 簡単な例として，unixのfindコマンドでは，findを，指定したパスの下にあるファイルのうち，以下の条件を満たすものを探す関数として扱っています．

  $ref_func
  

myfunc(func1)

-print
-exec {}\;
options are treated as other functions (ignore whether or not they are actually functions), the functions corresponding to these options are arguments to the find function, and whenever the find function finds a file name that matches the conditions, it executes
-print
function to output the file name
The return value of a function can also be another function. For example, the definition statement for the myfunc function is
function myfunc(){ . . return func1 }
.
In fact, functions that implement the above three functions are called first-order functions or higher-order functions, where higher-order functions must implement at least 2 and 3 above. there is no need to distinguish between first-order functions and higher-order functions, but if a distinction must be made, then.
first-order functions are more of a terminological concept that treats a function as a value that can be assigned out, passed as an argument, and returned as a value, and is used more for computer programming languages to describe whether a language supports first-order functions.
A higher-order function is a function type, like a callback function, and when a function meets the characteristics of a higher-order function, you can call it a higher-order function.
3. free variable and bound variable
This is a set of terms used in mathematics.
In computer programming languages, a free variable is a special kind of variable in a function that is neither defined in the function nor is it an argument to the function. In other words, it may be defined in an outer function but used in an inner function, so a free variable is often used interchangeably with a "non-local variable" (as anyone familiar with Python will know). For example
function func1(x){
 var z;
 function func2(y){
  return x+y+z # x and z are neither defined internally by func2, nor are they arguments to func2, so x and z are free variables
 }
 return func1
}

Free variables and bound variables correspond. A bound variable is a variable that was previously a free variable, but it will be assigned a value afterwards. After binding the free variable to a value, the variable becomes a bound variable or is called a bound variable.
For example.
function func1(x){
 var m=20 # For func2, this is the free variable to which the value is assigned, so m becomes the bound variable
 var z
 function func2(y){
  z=10 # Assign a value to the free variable z, z becomes the bound variable
  return m+x+y+z # m, x and z are all free variables
 }
 return func1
}

ref_func=func1(3) # assign a value to x, x becomes a bound variable

Callback functions
The callback function started out as a concept in C, which represents a function.
can access another function
When this function is finished, another function will be executed
That is, a function (B) is passed as an argument to another function (A), but when A is finished, B is called automatically, so this concept of callback functions is also called "call after".
But now callback functions are generic enough. Instead of calling function A after it finishes, we define where to call it ourselves.
For example, Perl's
File::Find
module, this function, together with the callback function, can do the same thing as the unix find command. For example, to search for a file in a directory and then print the name of that file, i.e.
find /path xxx -print
.
#! /usr/binuse File::Find;

sub print_path { # Define a function to output path names
 print "$File::Find::name\n";
}

$callback = \&print_path; # Create a function reference named $callback, so perl is a language that supports first-level functions

find( $callback,"/tmp" ); # Find the files under /tmp, and execute the $callback function once for each file found

passed here to the find function
$callback
is a callback function. A few key points.
$callback
is passed as an argument to another find() function (so the find() function is a higher-order function)
In the find() function, each time a file is found, this
$callback
function. Of course, if find is our own program, it is up to us to define where to call
$callback
$callback
is not called by us, but by the find() function in some cases (every time a file is found)
Callbacks are like fill-in-the-blank answers to functions, reusing the filled-in function to achieve a certain aspect of detail based on what we fill in, whereas normal functions are defined and can only mechanically reuse the function itself.
It is called a callback function because the function is not called by us subjectively and directly, but rather the function is taken as an argument and the function argument is called indirectly through the callee. Essentially, a callback function is no different from a normal function, except perhaps that it feels a little strange to define a function and never call it directly, so some people call it a "callback function" to refer to this indirect calling relationship in general.
Callback functions can be executed asynchronously by multiple threads.
Figuring out closures thoroughly
The concept of closures in computers was introduced from the world of mathematics, and in computer programming languages it is also known as lexical closures and function closures.
The simple, generic definition of a closure is that a function references a lexical variable that remains valid for the function that references it after the function or statement block ends (the variable's name disappears). There is a more rigorous definition of closures in the next section (from the wiki).
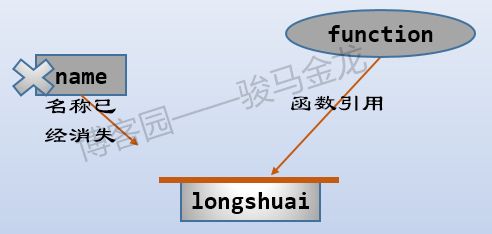Look at a python example: the function f is nested within the function g, and returns the function g
def f(x):
 def g(y):
  return x + y
 return g # return a closure: function with name (property of higher-order functions)

# Assign the closure function returned when the function is executed to a variable (a feature of higher-order functions)
a = f(1)

# Call the closure function stored in the variable
print (a(5))

# Instead of storing the closure in a temporary variable, just call the closure function once
print( f(1)(5) ) # f(1) is a closure function, because it is not assigned to a variable, so f(1) is called "anonymous closure"

The above a is a closure that is an instance of the function g(). f()'s argument x can be accessed by g. After f() returns the g function, f() exits and with it disappears the variable name x (note that it is the variable name x; the value of the variable does not necessarily disappear here yet). When the closure f(1) is assigned to a, the data object pointed to by the original x (i.e., value 1) is still referenced by the closure function pointed to by a. So the value 1 corresponding to x is still kept in memory after x disappears, and the value 1 pointed to by the original x disappears only when the closure named a is eliminated.
Closure feature 1: For each closure g() returned, different g()'s reference different data objects corresponding to x. In other words, the data objects corresponding to the variable x are independent of each other for each closure
For example, the following two closures are obtained, and although the free variables held in these two closures both reference equal values1, the two values are different data objects, and the two closures are also independent of each other.
a=f(1)
b=f(1)

Closure feature 2: For some closure function, as long as this is not an anonymous closure, then the closure function can always access the data object corresponding to x, even if the name x has disappeared
but
a=f(1) # The closure a, which has a name, will always reference the numeric object 1
a(3) # call the closure function a, will return 1 + 3 = 4, where 1 is the object being referenced by a, even if a(3) is not released after execution
a(3) # call the function a again, will return 4, where 1 and the above statement of 1 is the same data object
f(1)(3) # call the anonymous closure function, the data object 1 in f(1)(3) will disappear after the execution of
f(1)(3) # calls the anonymous closure function, which is independent of the anonymous closure above

The most important feature lies in the two executions of a(3) above: extending the lifecycle of lexical variables, but being safe enough to do so.
Look at the closure function in the perl program below to see the result more visually.
sub how_many { # Define the function
  my $count=2; # lexical variable $count
  return sub {print ++$count,"\n"}; # Return an anonymous function, which is an anonymous closure
}

$ref=how_many(); # Assign the closure to the variable $ref

how_many()->(); # (1) call an anonymous closure: output 3
how_many()->(); # (2) call anonymous closure: output 3
$ref->(); # (3) call named closure: output 3
$ref->(); # (4) call named closure again: output 4

The above assigns the closure to
$ref
by
$ref
to call this closure, even if the how_many
$count
disappears after how_many() is executed, but the
$ref
refers to a closure function that is still referencing the variable, so multiple calls to
$ref
will keep modifying the
$count
values, so (3) and (4) above output 3 first, then the changed 4. And (1) and (2) above both output 3, because the two how_many() functions return separate anonymous closures, and the data object 3 disappears after the statement is executed.
A stricter definition of closures
Note that a strictly defined closure is not the same as the preceding colloquially defined closure, and a colloquially defined closure does not necessarily match a strictly defined closure.
The stricter definition of a closure is a description (from the wiki) that no one can understand. As follows, a few keywords I've bolded because they're important.
Closures are a technique that enables the binding of variable names in lexical scopes in programming languages that support first-level functions. Operationally, a closure is a record used to hold a function and an environment. This environment record has some associative mapping that associates each free variable of the function with the value or reference of the name bound when the closure was created. With closures, even if the function is called from outside the scope, it allows functions to access those variables that have been captured by copying their values through the closure or by reference.
I know this is hard for anyone to understand, so in a nutshell: a function instance combined with an environment is a closure. This so-called environment determines the specificity of the function and the properties of the closure.
Or the python example above: function f is nested within function g, and returns function g
def f(x):
  def g(y):
    return x + y
  return g # Return a closure: function with name

# Assign the closure function returned when the function is executed to a variable
a = f(1)

The above a is a closure that is an instance of the function g(). f() has an argument x that can be accessed by g. For g(), this x is not defined internally by g() and is not an argument to g(), so this x is a free variable for g. Although the free variable is held in g(), the g() function itself is not a closure function. A closure function is created from g() only when the free variable x held by g is bound to the value of x passed to the f() function (i.e., the 1 in f(1)), which means that the closure function starts referencing the free variable, and the closure keeps holding the reference to this variable even after f() has finished executing. Then return this closure function in f(), because this closure function binds (references) the free variable x, which is the environment in which the closure function resides.
The environment is very important for closures, and is the key to distinguishing ordinary functions from closures. If instead of each closure returning holding free variables that belong to itself independently, all closures hold exactly the same free variables, then the closure can still be called a closure but is indistinguishable from a normal function. For example
def f(x):
  x=3
  def g(y):
    return x + y
  return g

a = f(1)
b = f(3)

In the above example, although x is a free variable, it is bound before the definition of g() (as introduced before, it is called a bound variable), making the closure a and closure b hold no longer free variables, but bound variables with the exact same value object of 3. There is really no difference between a and b at this point (although they are different objects). In other words, with closure a there is absolutely no need to define another closure b that is functionally identical.
In terms of function reusability, there is no difference between a and a normal function here; both simply reuse the function body. A true closure in the strictest sense, on the other hand, reuses the function body in addition to the environment in which it resides.
But in such a case, the returned g() is also a closure for a colloquially defined closure, but in a strictly defined closure, this is no longer considered a closure.
Look at another example: placing the free variable x after the text segment of the g() function definition.
def f(y):
  return x+y

x=1

def g(z):
  x=3
  return f(z)

print(g(1)) # output 2, not 4

The first thing to note is that python implements lexical scoping rules when no scope modifier is given, so the above
return f(z)
in f() sees the global variable x (because f() is defined in a global text segment), not x=3 in g().
Back to the closure problem. The above f() holds a free variable x. The text definition segment of this f(z) is in a global text segment, and the free variable x it binds is a global variable (declared and initialized to null or 0), but this variable is later assigned a value of 1. For each environment where f() is returned in g(), it holds the free variable x that is initially indeterminate, but is later determined to be 1. This situation cannot be called a closure either, because the closure is created when f() binds to the free variable, and by this time x is already a fixed value object.
Callback functions, closures, and anonymous functions
Callback functions, closures, and anonymous functions are not necessarily related, but because many books explain anonymous functions together with callback functions and closures, people mistakenly think that callback functions and closures need to be implemented through anonymous functions. In fact, an anonymous function is just a function that has a function definition text field but no name, while a closure is an instance of a function plus an environment (strictly speaking, a definition).
For closures and anonymous functions, still using python as an example.
def f(x):
  def g(y):
    return x + y
  return g # return a closure: a function with a name

def h(x):
  return lambda y: x + y # Return a closure: anonymous function

# Assign the closure function returned when the function is executed to a variable
a = f(1)
b = h(1)

# Call the closure function stored in the variable
print (a(5))
print (b(5))

For callback functions and anonymous functions, still using the perl find function as an example.
#! /usr/binuse File::Find;

$callback = sub {
  print "$File::Find::name\n";
}; # Create an anonymous function and its reference

find( $callback,"/tmp" ); # Find the files under /tmp, executing the $callback function once for each file found

Anonymous functions make the implementation of closures more concise, so many times the returned closure function is an instance of an anonymous function.
Summary
The above is all the content of this article, I hope the content of this article for your study or work has a certain reference learning value, if you have questions you can leave a message to exchange, thank you for your support of the Codedevlib.

-exec {}\;

-print

function myfunc(){ . . return func1 }

function func1(x){
 var z;
 function func2(y){
  return x+y+z # x and z are neither defined internally by func2, nor are they arguments to func2, so x and z are free variables
 }
 return func1
}

function func1(x){
 var m=20 # For func2, this is the free variable to which the value is assigned, so m becomes the bound variable
 var z
 function func2(y){
  z=10 # Assign a value to the free variable z, z becomes the bound variable
  return m+x+y+z # m, x and z are all free variables
 }
 return func1
}

ref_func=func1(3) # assign a value to x, x becomes a bound variable

File::Find

find /path xxx -print

#! /usr/binuse File::Find;

sub print_path { # Define a function to output path names
 print "$File::Find::name\n";
}

$callback = \&print_path; # Create a function reference named $callback, so perl is a language that supports first-level functions

find( $callback,"/tmp" ); # Find the files under /tmp, and execute the $callback function once for each file found

$callback

$callback

$callback

$callback

$callback

def f(x):
 def g(y):
  return x + y
 return g # return a closure: function with name (property of higher-order functions)

# Assign the closure function returned when the function is executed to a variable (a feature of higher-order functions)
a = f(1)

# Call the closure function stored in the variable
print (a(5))

# Instead of storing the closure in a temporary variable, just call the closure function once
print( f(1)(5) ) # f(1) is a closure function, because it is not assigned to a variable, so f(1) is called "anonymous closure"

a=f(1) # The closure a, which has a name, will always reference the numeric object 1
a(3) # call the closure function a, will return 1 + 3 = 4, where 1 is the object being referenced by a, even if a(3) is not released after execution
a(3) # call the function a again, will return 4, where 1 and the above statement of 1 is the same data object
f(1)(3) # call the anonymous closure function, the data object 1 in f(1)(3) will disappear after the execution of
f(1)(3) # calls the anonymous closure function, which is independent of the anonymous closure above

sub how_many { # Define the function
  my $count=2; # lexical variable $count
  return sub {print ++$count,"\n"}; # Return an anonymous function, which is an anonymous closure
}

$ref=how_many(); # Assign the closure to the variable $ref

how_many()->(); # (1) call an anonymous closure: output 3
how_many()->(); # (2) call anonymous closure: output 3
$ref->(); # (3) call named closure: output 3
$ref->(); # (4) call named closure again: output 4

$ref

$count

$count

def f(x):
  def g(y):
    return x + y
  return g # Return a closure: function with name

# Assign the closure function returned when the function is executed to a variable
a = f(1)

def f(x):
  x=3
  def g(y):
    return x + y
  return g

a = f(1)
b = f(3)

def f(y):
  return x+y

x=1

def g(z):
  x=3
  return f(z)

print(g(1)) # output 2, not 4