[解決済み] グラフにおいて最小容量が最大となる経路の探索

質問

ある友人が仕事関連のプロジェクトで、ノードaからノードbまでのエッジが持つ最大容量を計算する必要があります。しかし、aからbへの経路の最大容量は、最も低い容量を持つエッジによって制限されています。

簡単なサンプルで説明します。

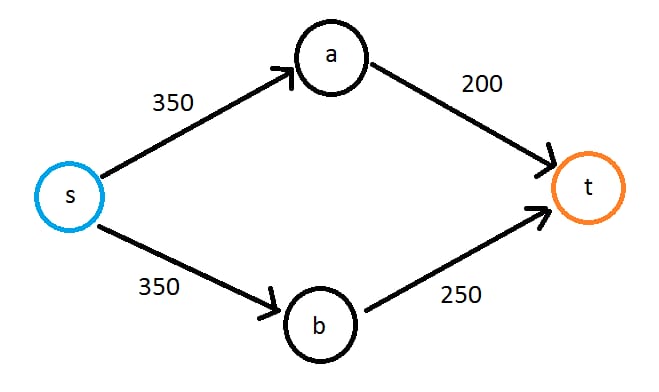
つまり、グラフは重み付きエッジを持つ有向グラフで、循環することもあります。最も容量の大きいパスは、s->b->tで、そのエッジが上限を設定しているので、250の容量を持つことになります。

少し読んでみたところ、この種の問題は "ワイドパス問題" あるいは、最大最小の容量を持つ道といったところでしょうか。しかし、これにどう取り組むかを説明する例や疑似コードは見当たりません。

BFSを使って、sからtまでのすべての経路を見つけ、何とか経路の中で一度だけノードを訪れることを許し、その経路の中の最小値を見つける、というようなことを考えていたのですが、うまくいきますか？

どのように解決するのですか？

の変形を使用します。 ダイクストラの . 以下の擬似コードはWikipediaから直接引用し、5つの小さな点を変更しただけです。

1. 名前を変更 dist から width (3行目以降)
2. 各初期化 width を -infinity (3行目)
3. ソースの幅を初期化し infinity (8行目)
4. 終了基準を -infinity (14行目)
5. 更新関数と符号の修正（20＋21行目）

1  function Dijkstra(Graph, source):
2      for each vertex v in Graph:                                 // Initializations
3          width[v] := -infinity  ;                                // Unknown width function from 
4                                                                  // source to v
5          previous[v] := undefined ;                              // Previous node in optimal path
6      end for                                                     // from source
7      
8      width[source] := infinity ;                                 // Width from source to source
9      Q := the set of all nodes in Graph ;                        // All nodes in the graph are
10                                                                 // unoptimized – thus are in Q
11      while Q is not empty:                                      // The main loop
12          u := vertex in Q with largest width in width[] ;       // Source node in first case
13          remove u from Q ;
14          if width[u] = -infinity:
15              break ;                                            // all remaining vertices are
16          end if                                                 // inaccessible from source
17          
18          for each neighbor v of u:                              // where v has not yet been 
19                                                                 // removed from Q.
20              alt := max(width[v], min(width[u], width_between(u, v))) ;
21              if alt > width[v]:                                 // Relax (u,v,a)
22                  width[v] := alt ;
23                  previous[v] := u ;
24                  decrease-key v in Q;                           // Reorder v in the Queue
25              end if
26          end for
27      end while
28      return width;
29  endfunction

なぜこの方法が有効なのかを（手抜きで）説明すると、ソースから始めるのです。そこから、それ自体には無限の容量があります。次に、ソースの近傍をすべてチェックします。エッジがすべて同じ容量を持っていないと仮定します（この例では (s, a) = 300 ). そうすると b を経由して (s, b) の最適な容量がわかります。 b . そして、すべての頂点に到達するまで、既知の頂点の集合の最隣接点を回り続けるのです。