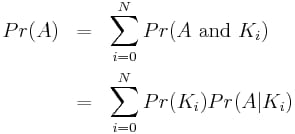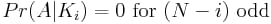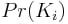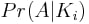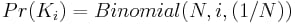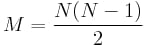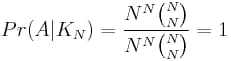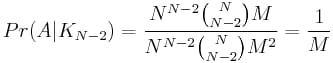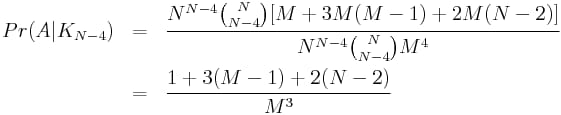配列が変わらない確率は何％か？

2023-11-06 04:52:31

質問

この質問は、マイクロソフトの面接で聞かれたものです。なぜこのような確率に関する奇妙な質問をするのか、非常に興味があります。

0からN-1までの乱数を生成する乱数発生器、rand(N)が与えられたとき。

int A[N]; // An array of size N
for(i = 0; i < N; i++)
{
    int m = rand(N);
    int n = rand(N);
    swap(A[m],A[n]);
}

EDITです。 種が確定していないことに注意。

配列Aが変わらない確率は？

配列に一意な要素が含まれていると仮定する。

どのように解決するのですか？

_{さて、私はこの問題を少し楽しみました。最初に問題を読んだときに思いついたのは群論（対称群S
_n
特に）である。forループは単純に順列σをS
_n
の並べ換えσを作るだけである。私の数学はそれほど華々しくなく、少し錆びついているので、私の表記がずれていたら、ご容赦ください。}

概要

説明 A は、並べ替えの後に配列が変化しない事象とします。私たちは最終的に事象 A , Pr(A) .

私の解決策は、以下の手順に従おうとするものです。

すべての可能な並べ替え (配列の並べ替え) を検討します。
これらの並べ替えを 不連続 の数に基づいて、いわゆる 同一性転置 の数に基づく集合です。これにより、この問題は であっても の並べ換えだけにすることができます。
並べ換えが偶数（かつ特定の長さ）であることを条件として、恒等並べ換えを得る確率を決定する。
配列が変化しない全体的な確率を得るために、これらの確率を合計する。

1) 考えられる結果

forループの各反復は、スワップ(または転置を作成し、その結果は2つのうちの1つです。

2 つの要素が入れ替わります。
要素がそれ自身と入れ替わります。我々の意図と目的からすると、配列は変更されません。

2番目のケースにラベルを付けます。を定義してみましょう。 同一性転置 を次のように定義します。

以下は 同一性転置 は、ある数字がそれ自身と入れ替わるときに発生します。つまり、上記の for ループで n == m となるときです。

リストされたコードの任意の実行に対して、我々は N の転置を行います。あるのは 0, 1, 2, ... , N はこの連鎖に現れる同一性転置の

例えば N = 3 のケースを考えてみましょう。

Given our input [0, 1, 2].
Swap (0 1) and get [1, 0, 2].
Swap (1 1) and get [1, 0, 2]. ** Here is an identity **
Swap (2 2) and get [1, 0, 2]. ** And another **

同一でない転置が奇数個（1個）あり、配列が変化していることに注意してください。

2) 同一性転置の数に基づく分割

以下のように K_i という事象が発生します。 i が現れる事象である。これは、すべての可能な結果の網羅的な分割を形成することに注意してください。

いかなる順列も 2 つの異なる量の同一性転置を同時に持つことはできない。
すべての可能な並べ換えは 0 と N の同一性転置。

このように、私たちは総確率の法則 :

これでようやくパーティションを利用できるようになりました。なお、このとき 非同一性 の転置の数が奇数であるとき、配列が変化しないことはありえないことに注意してください*。このように

* _{群論より、順列は偶数か奇数であるが、両方はありえない。したがって、奇数順列は恒等順列になることはできない（恒等順列は偶数であるから）。}

3) 確率の決定

では、次の2つの確率を決定する必要があります。 N-i の2つの確率を決定する必要があります。

第1期

第1ターム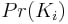を持つ並べ換えが得られる確率を表している。 i の同一性転置があります。これは、forループの各反復に対してなので、2項であることがわかります。

結果はその前の結果とは無関係であり
同一性転置を作る確率は同じである、すなわち 1/N .

このように N が得られる確率は i の同一性転置が得られる。

第2期

というわけで、ここまでくれば、この問題はに対して N - i である。これは、次のような場合に ID 並べ換えが得られる確率を表しています。 i の転置が恒等式である場合の恒等順列を得る確率を表している。私は可能な並べ換えの数の上に ID 並べ換えを達成する方法の数を決定するために素朴なカウントのアプローチを使用します。

まず、並べ換えを考えてみましょう。 (n, m) と (m, n) と等価である。では M が可能な非同一の並べ換えの数であるとします。私たちはこの量を頻繁に使用します。

ここでの目標は、転置のコレクションを組み合わせて恒等順列を形成することができる方法の数を決定することです。の例と一緒に一般的な解を構築してみることにします。 N = 4 .

を考えてみましょう。 N = 4 の場合、すべての同一性転置( すなわち i = N = 4 ). ここで X は同一性転置を表すとする。各 X には N の可能性がある（それらは n = m = 0, 1, 2, ... , N - 1 ). したがって、そこには N^i = 4^4 を達成する可能性がある。完全を期すために、二項係数を追加する。 C(N, i) を加えて、恒等転置の順序を検討します（ここでは単に 1 に等しい）。以下では、上に要素の物理的なレイアウト、下に可能性の数でこれを表現してみました。

I  =  _X_   _X_   _X_   _X_
       N  *  N  *  N  *  N  * C(4, 4) => N^N * C(N, N) possibilities

今度は明示的に代入せずに N = 4 と i = 4 というように、一般的な場合について見てみましょう。上記を先に求めた分母と組み合わせると、次のようになる。

これは直感的なものです。実際には 1 以外の値を指定すると、おそらく心配になるでしょう。考えてみてください：私たちは、すべての N の転置はすべて恒等式であると言われています。この状況で配列が変化しないのはなぜでしょうか？明らかに 1 .

さて、再び N = 4 に対して、2つの同一性転置( すなわち i = N - 2 = 2 ). 慣例として、2つの恒等式を最後に配置します（順番は後で決めます）。これで、合成すると恒等並べ換えとなる2つの転置を選ぶ必要があることがわかりました。任意の要素を最初の場所に配置し、それを t1 . 上で述べたように M とする可能性があります。 t1 が ID ではないとします（すでに 2 つ配置しているのでありえません）。

I  =  _t1_   ___   _X_   _X_
       M   *  ?  *  N  *  N

2番目の場所に入る可能性のある唯一の要素は、逆数の t1 であり、実際には t1 である(そしてこれは逆数の一意性によって唯一のものである)。この場合、4つの場所が空いていて、2つの同一順列を置きたいと考えています。何通りあるでしょうか。4は2を選びます。

I  =  _t1_   _t1_   _X_   _X_ 
       M   *  1   *  N  *  N  * C(4, 2) => C(N, N-2) * M * N^(N-2) possibilities

再び一般的な場合を見てみると、これは全てに対応しています。

最後に N = 4 のケースで、同一性転置がない場合 ( すなわち i = N - 4 = 0 ). 多くの可能性があるため、トリッキーになり始め、ダブルカウントしないように注意する必要があります。同じように、1つの要素を最初の場所に置き、可能な組み合わせを考えることから始めます。まず、最も簡単な方法として、同じ転置を4回行うことを考えます。

I  =  _t1_   _t1_   _t1_   _t1_ 
       M   *  1   *  1   *  1   => M possibilities

ここで、2つのユニークな要素について考えてみましょう。 t1 と t2 . があり M の可能性があります。 t1 のみであり M-1 の可能性があります。 t2 (ただし t2 とは等しくできません。 t1 ). すべての配置を洗い出すと、次のようなパターンが残ります。

I  =  _t1_   _t1_   _t2_   _t2_ 
       M   *  1   *  M-1 *  1   => M * (M - 1) possibilities   (1)st

   =  _t1_   _t2_   _t1_   _t2_
       M   *  M-1 *  1   *  1   => M * (M - 1) possibilities   (2)nd

   =  _t1_   _t2_   _t2_   _t1_
       M   *  M-1 *  1   *  1   => M * (M - 1) possibilities   (3)rd

では、3つのユニークな要素について考えてみましょう。 t1 , t2 , t3 . を配置しましょう。 t1 を最初に置き、次に t2 . 例によって、あります。

I  =  _t1_   _t2_   ___   ___ 
       M   *  ?   *  ?  *  ?

私たちはまだ、どれだけの数の可能な t2 がいくつあり得るかはまだ言えません。その理由はすぐにわかります。

私たちは今 t1 を3番目の場所に置きます。注目してください。 t1 がそこになければならないことに注意してください。なぜなら、もし最後の場所に行くのであれば、単に (3)rd の配置を再現することになるからです。ダブルカウントはよくありません。これで3番目のユニークな要素 t3 が最後の位置になります。

I  =  _t1_   _t2_   _t1_   _t3_ 
       M   *  ?   *  1  *   ?

では、なぜ、1分ほどで、その数の t2 の数をより詳細に検討する必要があったのでしょうか。転置された t1 と t2 はできない は、不連続な並べ換えである ( すなわち のうちの 1 つを共有しなければなりません（等しくすることもできないので 1 つだけです）。 n または m ). この理由は、もしこれらが不連続であれば、並べ替えの順番を入れ替えることができるからです。つまり、2重にカウントすることになり (1)st の配置を二重にカウントすることになります。

セイ t1 = (n, m) . t2 は、次のような形式でなければなりません。 (n, x) または (y, m) に対して、いくつかの x と y を非連接とする。ただし x は n または m そして y でないものも多くあります。 n または m . という順列の可能性の数です。 t2 があり得る順列の数は、実際には 2 * (N - 2) .

では、レイアウトに戻りましょう。

I  =  _t1_    _t2_    _t1_   _t3_ 
       M   * 2(N-2) *  1   *  ?

現在 t3 の合成の逆でなければならない。 t1 t2 t1 . 手作業でやってみましょう。

(n, m)(n, x)(n, m) = (m, x)

このように t3 は、必ず (m, x) . これは ではなく に不一致 t1 と等しくなく、かつ t1 または t2 であるため、この場合は二重にカウントされることはありません。

I  =  _t1_    _t2_    _t1_   _t3_ 
       M   * 2(N-2) *  1  *   1    => M * 2(N - 2) possibilities

最後に、これらをすべてまとめて

4) まとめる

というわけで、これで終わりです。逆算して、わかったことを手順2で出した元の和に代入します。を計算したところ、答えは N = 4 の場合の答えを計算しました。これは、別の答えで見つかった経験的な数値と非常によく一致します!

         N = 4
         M = 6 _________ _____________ _________
                  | Pr(K_i) | Pr(A | K_i) | プロダクト｜。
         _________|_________|_____________|_________|
        
        | i = 0 | 0.316 | 120 / 1296 | 0.029 |
        |_________|_________|_____________|_________|
        
        | i = 2 | 0.211 | 6 / 36 | 0.035 |
        |_________|_________|_____________|_________|
        
        | i = 4 | 0.004 | 1 / 1 | 0.004 |
        |_________|_________|_____________|_________|
                            
                            | サム    | 0.068 |
                            |_____________|_________|

正しさ

群論でここに適用できる結果があればクールなのですが、多分あるのでしょう! それは確かに、このすべての退屈なカウントを完全になくすのに役立つでしょう (そして、この問題をもっとエレガントなものに短縮するのにも役立つでしょう)。私は N = 4 . については N > 5 については、与えられたものは近似値を与えるだけです（どの程度良いかは分かりません）。その理由はよく考えればわかることです。 N = 8 の転置がある場合、明らかに 4 で同一視する方法があることは明らかです。順列が長くなるにつれて、その数は数えるのが難しくなるようです（私が知る限りでは...）。

とにかく、こんなことは面接の範囲内では絶対にできないんです。運が良ければ分母のステップまではいけるだろうけど。その先は、かなり厄介なことになりそうです。