数式を簡略化するためのストラテジー

2023-09-18 10:55:58

質問

数式を表す整形された木があります。例えば、文字列が与えられると "1+2-3*4/5" という文字列があると、これは次のようにパースされます。

subtract(add(1,2),divide(multiply(3,4),5))

というのは、このツリーのように表現されます。

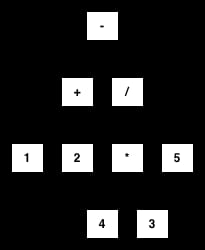
この木をできるだけ小さくすることができればと思います。上記の場合、すべての数値が定数であるため、これは非常に簡単です。しかし、一旦未知数(unknown)を許容すると、物事はより複雑になり始めます。 $ の後に識別子が続く)。

"3*$a/$a" は divide(multiply(3,$a), $a)

これを単純化すると 3 となるはずです。 $a の項は互いに相殺されるはずだからです。問題は、これを一般的な方法で認識するにはどうしたらいいかということです。 min(3, sin($x)) は常に sin($x) ? を認識するにはどうすればよいのでしょうか？ sqrt(pow($a, 2)) は abs($a) ? を認識するにはどうすればよいのでしょうか？ nthroot(pow(42, $a), $a) (その ^th のルートは、42 から a ^th 乗)は 42 ?

この質問がかなり広範であることは承知していますが、しばらくこれに頭を打ち付けていて、十分満足のいくものが出てきません。

どのように解決するのですか？

あなたはおそらく項書換えシステム . 基礎となる数学については、以下のサイトを参照してください。ウィキペディア .

term rewrite モジュールの構造

最近、解決策を実装したので...

まず、式の構造をモデル化したクラスCExpressionを用意します。
実装 CRule これはパターンと置換を含む。パターン変数として特殊な記号を使用し、パターンマッチの際に束縛され、置換式で置換される必要がある。
次に、クラス CRule . このクラスのメインメソッド applyRule(CExpression, CRule) は、expression の任意の適用可能な部分式に対して、ルールのマッチングを試みます。マッチした場合は、その結果を返す。
最後に、クラスを実装します。 CRuleSet を実装します。これは単に CRule オブジェクトの集合です。メインメソッド reduce(CExpression) は，これ以上ルールが適用できない限り，一連のルールを適用し，縮小された式を返す．
さらに、クラス CBindingEnvironment というクラスが必要で、これは既にマッチしたシンボルをマッチした値にマップします。

式を正規の形に書き換えてみる

この方法はある時点までは有効ですが、完全ではない可能性があることを忘れないでください。これは、以下のすべてのルールが局所的な項の書き換えを実行するという事実によるものです。

この局所的な書き換えロジックをより強固なものにするために、式を私が正規形と呼ぶものに変換することを試みる必要があります。これは私のアプローチです。

用語にリテラル値が含まれる場合、その用語をできるだけ右に移動するようにします。
最終的には、このリテラル値は一番右に表示され、完全にリテラルな式の一部として評価されることがあります。

完全なリテラル表現を評価する場合

面白いのは、完全なリテラル式をいつ評価するかということです。例えば、次のような式があったとします。

   x * ( 1 / 3 )

となり、以下のようになります。

   x * 0.333333333333333333

ここで、x を 3 に置き換えたとすると、次のようになります。

   0.999999999999999999999999

このように、eagerの評価では少し不正確な値が返されます。

一方、( 1 / 3 )のまま、まず x を 3 で置き換えると

   3 * ( 1 / 3 )

リライトルールでは

このように、完全にリテラルな表現を遅く評価することは有用かもしれません。

リライトルールの例

私のルールがアプリケーションの中でどのように表示されるかは、以下の通りです。1, _2, ...の記号は任意の部分式にマッチします。

addRule( new TARuleFromString( '0+_1',   // left hand side  :: pattern
                               '_1'      // right hand side :: replacement
                             ) 
       );

あるいはもう少し複雑な

addRule( new TARuleFromString( '_1+_2*_1', 
                               '(1+_2)*_1' 
                             ) 
       );

ある種の特殊記号は、特殊な部分式にのみマッチします。例えば、_Literal1, _Literal2, ...はリテラル値のみにマッチします。

addRule( new TARuleFromString( 'exp(_Literal1) * exp(_Literal2 )', 
                               'exp( _Literal1 + _Literal2 )' 
                             ) 
       );

このルールは、非リテラルな表現を左に移動させる。

addRule( new TARuleFromString( '_Literal*_NonLiteral', 
                               '_NonLiteral*_Literal' 
                             ) 
       );

'_'で始まる名前はすべてパターン変数である。システムはルールにマッチする間、既にマッチしたシンボルの代入のスタックを保持します。

最後に、ルールが非終端置換シーケンスを生成する可能性があることを忘れないでください。したがって、式を減らしている間、どの中間式が以前に到達したかをプロセスに記憶させる。

私の実装では、中間式は直接保存しません。中間式のMD5()ハッシュを配列にして保存しています。

出発点となるルール群

ここでは、出発点となるルールセットを紹介します。

            addRule( new TARuleFromString( '0+_1', '_1' ) );
            addRule( new TARuleFromString( '_Literal2=0-_1', '_1=0-_Literal2' ) );
            addRule( new TARuleFromString( '_1+0', '_1' ) );
            
            addRule( new TARuleFromString( '1*_1', '_1' ) );
            addRule( new TARuleFromString( '_1*1', '_1' ) );
            
            addRule( new TARuleFromString( '_1+_1', '2*_1' ) );
            
            addRule( new TARuleFromString( '_1-_1', '0' ) );
            addRule( new TARuleFromString( '_1/_1', '1' ) );
            
            // Rate = (pow((EndValue / BeginValue), (1 / (EndYear - BeginYear)))-1) * 100 

            addRule( new TARuleFromString( 'exp(_Literal1) * exp(_Literal2 )', 'exp( _Literal1 + _Literal2 )' ) );
            addRule( new TARuleFromString( 'exp( 0 )', '1' ) );
            
            addRule( new TARuleFromString( 'pow(_Literal1,_1) * pow(_Literal2,_1)', 'pow(_Literal1 * _Literal2,_1)' ) );
            addRule( new TARuleFromString( 'pow( _1, 0 )', '1' ) );
            addRule( new TARuleFromString( 'pow( _1, 1 )', '_1' ) );
            addRule( new TARuleFromString( 'pow( _1, -1 )', '1/_1' ) );
            addRule( new TARuleFromString( 'pow( pow( _1, _Literal1 ), _Literal2 )', 'pow( _1, _Literal1 * _Literal2 )' ) );

//          addRule( new TARuleFromString( 'pow( _Literal1, _1 )', 'ln(_1) / ln(_Literal1)' ) );
            addRule( new TARuleFromString( '_literal1 = pow( _Literal2, _1 )', '_1 = ln(_literal1) / ln(_Literal2)' ) );
            addRule( new TARuleFromString( 'pow( _Literal2, _1 ) = _literal1 ', '_1 = ln(_literal1) / ln(_Literal2)' ) );

            addRule( new TARuleFromString( 'pow( _1, _Literal2 ) = _literal1 ', 'pow( _literal1, 1 / _Literal2 ) = _1' ) );
            
            addRule( new TARuleFromString( 'pow( 1, _1 )', '1' ) );

            addRule( new TARuleFromString( '_1 * _1 = _literal', '_1 = sqrt( _literal )' ) );
            
            addRule( new TARuleFromString( 'sqrt( _literal * _1 )', 'sqrt( _literal ) * sqrt( _1 )' ) );
            
            addRule( new TARuleFromString( 'ln( _Literal1 * _2 )', 'ln( _Literal1 ) + ln( _2 )' ) );
            addRule( new TARuleFromString( 'ln( _1 * _Literal2 )', 'ln( _Literal2 ) + ln( _1 )' ) );
            addRule( new TARuleFromString( 'log2( _Literal1 * _2 )', 'log2( _Literal1 ) + log2( _2 )' ) );
            addRule( new TARuleFromString( 'log2( _1 * _Literal2 )', 'log2( _Literal2 ) + log2( _1 )' ) );
            addRule( new TARuleFromString( 'log10( _Literal1 * _2 )', 'log10( _Literal1 ) + log10( _2 )' ) );
            addRule( new TARuleFromString( 'log10( _1 * _Literal2 )', 'log10( _Literal2 ) + log10( _1 )' ) );

            addRule( new TARuleFromString( 'ln( _Literal1 / _2 )', 'ln( _Literal1 ) - ln( _2 )' ) );
            addRule( new TARuleFromString( 'ln( _1 / _Literal2 )', 'ln( _Literal2 ) - ln( _1 )' ) );
            addRule( new TARuleFromString( 'log2( _Literal1 / _2 )', 'log2( _Literal1 ) - log2( _2 )' ) );
            addRule( new TARuleFromString( 'log2( _1 / _Literal2 )', 'log2( _Literal2 ) - log2( _1 )' ) );
            addRule( new TARuleFromString( 'log10( _Literal1 / _2 )', 'log10( _Literal1 ) - log10( _2 )' ) );
            addRule( new TARuleFromString( 'log10( _1 / _Literal2 )', 'log10( _Literal2 ) - log10( _1 )' ) );
            
        
            addRule( new TARuleFromString( '_Literal1 = _NonLiteral + _Literal2', '_Literal1 - _Literal2 = _NonLiteral' ) );
            addRule( new TARuleFromString( '_Literal1 = _NonLiteral * _Literal2', '_Literal1 / _Literal2 = _NonLiteral' ) );
            addRule( new TARuleFromString( '_Literal1 = _NonLiteral / _Literal2', '_Literal1 * _Literal2 = _NonLiteral' ) );
            addRule( new TARuleFromString( '_Literal1 =_NonLiteral - _Literal2',  '_Literal1 + _Literal2 = _NonLiteral' ) );

            addRule( new TARuleFromString( '_NonLiteral + _Literal2 = _Literal1 ', '_Literal1 - _Literal2 = _NonLiteral' ) );
            addRule( new TARuleFromString( '_NonLiteral * _Literal2 = _Literal1 ', '_Literal1 / _Literal2 = _NonLiteral' ) );
            addRule( new TARuleFromString( '_NonLiteral / _Literal2 = _Literal1 ', '_Literal1 * _Literal2 = _NonLiteral' ) );
            addRule( new TARuleFromString( '_NonLiteral - _Literal2 = _Literal1',  '_Literal1 + _Literal2 = _NonLiteral' ) );
            
            addRule( new TARuleFromString( '_NonLiteral - _Literal2 = _Literal1 ', '_Literal1 + _Literal2 = _NonLiteral' ) );
            addRule( new TARuleFromString( '_Literal2 - _NonLiteral = _Literal1 ', '_Literal2 - _Literal1 = _NonLiteral' ) );
            
            addRule( new TARuleFromString( '_Literal1 = sin( _NonLiteral )', 'asin( _Literal1 ) = _NonLiteral' ) );
            addRule( new TARuleFromString( '_Literal1 = cos( _NonLiteral )', 'acos( _Literal1 ) = _NonLiteral' ) );
            addRule( new TARuleFromString( '_Literal1 = tan( _NonLiteral )', 'atan( _Literal1 ) = _NonLiteral' ) );

            addRule( new TARuleFromString( '_Literal1 = ln( _1 )', 'exp( _Literal1 ) = _1' ) );
            addRule( new TARuleFromString( 'ln( _1 ) = _Literal1', 'exp( _Literal1 ) = _1' ) );
            
            addRule( new TARuleFromString( '_Literal1 = _NonLiteral', '_NonLiteral = _Literal1' ) );

            addRule( new TARuleFromString( '( _Literal1 / _2 ) = _Literal2', '_Literal1 / _Literal2 = _2 ' ) );
            
            addRule( new TARuleFromString( '_Literal*_NonLiteral', '_NonLiteral*_Literal' ) );
            addRule( new TARuleFromString( '_Literal+_NonLiteral', '_NonLiteral+_Literal' ) );
            
            addRule( new TARuleFromString( '_Literal1+(_Literal2+_NonLiteral)', '_NonLiteral+(_Literal1+_Literal2)' ) );
            addRule( new TARuleFromString( '_Literal1+(_Literal2+_1)', '_1+(_Literal1+_Literal2)' ) );

            addRule( new TARuleFromString( '(_1*_2)+(_3*_2)', '(_1+_3)*_2' ) );
            addRule( new TARuleFromString( '(_2*_1)+(_2*_3)', '(_1+_3)*_2' ) );

            addRule( new TARuleFromString( '(_2*_1)+(_3*_2)', '(_1+_3)*_2' ) );
            addRule( new TARuleFromString( '(_1*_2)+(_2*_3)', '(_1+_3)*_2' ) );
            
            addRule( new TARuleFromString( '(_Literal * _1 ) / _Literal', '_1' ) );
            addRule( new TARuleFromString( '(_Literal1 * _1 ) / _Literal2', '(_Literal1 * _Literal2 ) / _1' ) );
            
            addRule( new TARuleFromString( '(_1+_2)+_3', '_1+(_2+_3)' ) );
            addRule( new TARuleFromString( '(_1*_2)*_3', '_1*(_2*_3)' ) );

            addRule( new TARuleFromString( '_1+(_1+_2)', '(2*_1)+_2' ) );

            addRule( new TARuleFromString( '_1+_2*_1', '(1+_2)*_1' ) );

            addRule( new TARuleFromString( '_literal1 * _NonLiteral = _literal2', '_literal2 / _literal1 = _NonLiteral' ) );
            addRule( new TARuleFromString( '_literal1 + _NonLiteral = _literal2', '_literal2 - _literal1 = _NonLiteral' ) );
            addRule( new TARuleFromString( '_literal1 - _NonLiteral = _literal2', '_literal1 - _literal2 = _NonLiteral' ) );
            addRule( new TARuleFromString( '_literal1 / _NonLiteral = _literal2', '_literal1 * _literal2 = _NonLiteral' ) );

ルールをファーストクラス式にする

興味深い点です。上記のルールは特殊な式であり、式パーサーによって正しく評価されるため、ユーザーは新しいルールを追加することもでき、アプリケーションの書き換え機能を強化することができます。

式 (またはより一般的な: 言語) の解析

については Cocoa/OBjCアプリケーション , Dave DeLongのDDMathParser は数式を構文解析するのに最適な候補です。

他の言語については、古くからの友人である Lex & Yacc あるいは、より新しい GNU Bison が参考になるかもしれません。

はるかに若い、そして構文ファイルの膨大なセットを使用することができます。 , ANTLR は、Java をベースとした最新のパーサージェネレータです。純粋にコマンドラインで使用する以外に ANTLRワークスを提供しています。 GUI フロントエンド を提供し、ANTLR ベースのパーサーの構築とデバッグを行います。ANTLR は、以下のような文法を生成します。様々なホスト言語のような JAVA、C、Python、PHP、C#のいずれか。 . ActionScript ランタイムは、現在が壊れています。 .

万が一、あなたが 式のパース方法を学びたい場合 (あるいは一般的な言語)をボトムアップで学びたいのであれば、私は次のようなものを提案したいと思います。 Niklaus Wirthによる無料の書籍のテキスト (あるいはドイツ語版 )、PascalとModula-2の発明者として有名です。

数式を簡略化するためのストラテジー

質問

どのように解決するのですか？

関連

[解決済み】Quickselectの時間の複雑さを説明する

[解決済み] NPとco-NPの違いは何ですか？

[解決済み] アルゴリズムの教科書では、ソートされた配列について「増加」ではなく「非減少」を使っているのはなぜですか？

[解決済み] ゲーム「2048」の最適なアルゴリズムとは？

[解決済み] NaN値をチェックするにはどうすればよいですか？

[解決済み] 文字列で指定された数式を評価するには？

[解決済み】画像処理。コカ・コーラ缶」認識のためのアルゴリズム改良

[解決済み】C言語ではsin()などの数学関数はどのように計算されるのですか？

[解決済み] MapReduceのソートアルゴリズムはどのように動作するのですか？

[解決済み] ユークリッド・アルゴリズムの時間計算量

最新

nginxです。[emerg] 0.0.0.0:80 への bind() に失敗しました (98: アドレスは既に使用中です)

htmlページでギリシャ文字を使うには

ピュアhtml+cssでの要素読み込み効果

純粋なhtml + cssで五輪を実現するサンプルコード

ナビゲーションバー・ドロップダウンメニューのHTML+CSSサンプルコード

タイピング効果を実現するピュアhtml+css

htmlの選択ボックスのプレースホルダー作成に関する質問

html css3 伸縮しない画像表示効果

トップナビゲーションバーメニュー作成用HTML+CSS

html+css 実装サイバーパンク風ボタン

おすすめ

[解決済み] クイックソートとヒープソートの比較

[解決済み] Bogosort (a.k.a Monkey Sort)よりも悪いソートアルゴリズムはあるのか？[クローズド］

[解決済み] 与えられた数列の中に現れない最小の正の整数を求めよ。

[解決済み] クイックソートピボットの選択

[解決済み] ユダヤ人の足の爪を切る最適なアルゴリズムとは？

[解決済み] 並べ換え→数→並べ換えの高速マッピングアルゴリズム

[解決済み] 式（エクスプレッション）パーサー（優先順位付き）？

[解決済み] 与えられた範囲にあるすべての数値のXORを求めよ

[解決済み] Dijkstraのアルゴリズムはなぜdecrease-keyを使うのですか？

[解決済み] アルゴリズムで見慣れない記号：∀は何を意味するのか？[クローズド］