html5 applet fly into the shopping cart (放物線描画モーショントラック・ポイント)
序文:最近、小さなプログラムを行う過程で友人が、ショッピングカートの効果関数に飛ぶを開発する必要性に遭遇した。このような状況のためにいくつかのオンラインデモは、多かれ少なかれ問題(バグ)のシナリオを満たしていないでしょう、この状況のために私は友人が問題を解決するためにプログラムを書くのを助けることにしました。
何を実装するか考えていますか?超簡単です
アプレットにしろ、h5のフライインカートにしろ、何もかもが 平投げ または アップスロー いずれの場合も、中学生から放物線理論を学び始めることは全く可能ですし、高校1年生の物理の自由落下運動は、放物線理論を具体的に具現化したものと言えます。
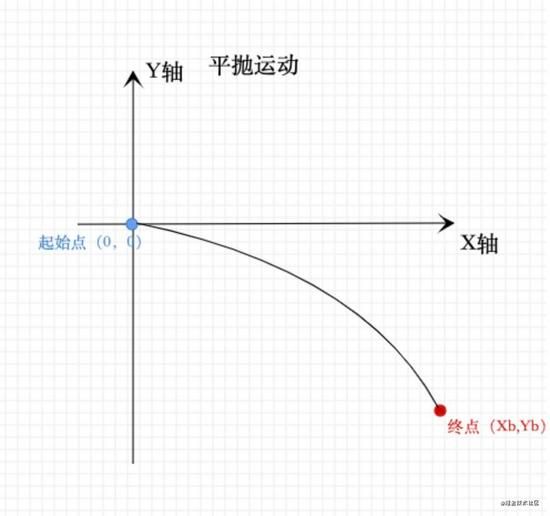
放物線運動
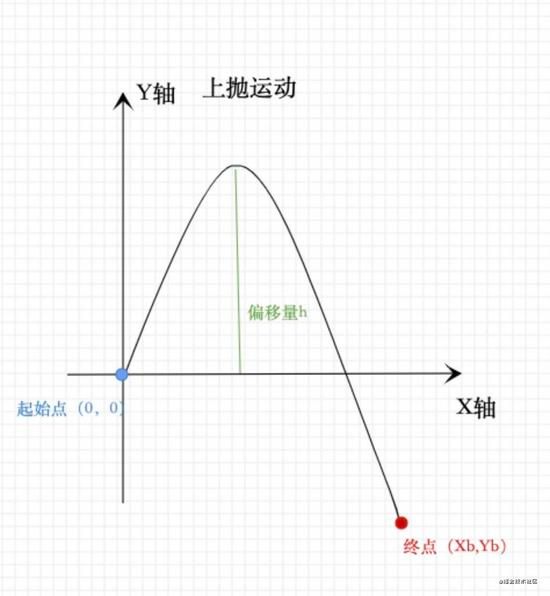
アップスローモーション
仮想直角座標系の構築、放物線プロットの軌跡点
このソリューションの本質は、ショッピングカートの始点と終点に合わせて、始点と終点を放物線の2点とし、始点を直角座標系(0、0)とすることで、その後の他の座標点の演算を容易にするセンスである。もう一つ注意すべきは、hオフセットを投げるように設定されている場合、最高点(頂点)の座標が必要であることです。
/**
* Fly-in cart, track point drawing
* @author ????
* @param {Array} start` Insert code snippet here `Point starting point clientX, clientY values (required)
* @param {Array} endPoint endpoint clientX, clientY values (required)
* @param {number} point Number of points (required)
* @param {number} h the height of the parabola upwards (upward motion) (optional)
* @param {number} hclientX The value of clientX when the highest point is reached in the presence of h.
* @return {Array} [ left ,top ] array of values
*/
function flycart(startPoint, endPoint, point, h = 0, hclientX) {
/*
Set startPoint to (0,0), the parabola passes through (0,0), and the model relation y = ax^2 + bx or y = ax^ 2 can be derived.
1 When there is h, the parabola will be shifted upward by h on the y-axis, in which case the relation y = ax^2 + bx
2 When there is no h, the parabola startPoint is the vertex, and the relation y = ax^2
*/
/* Parameter validation */
function Validityparameter() {
let isOkey = true
Array.isArray(startPoint) && startPoint.length ! == 2 && (isOkey = false)
Array.isArray(endPoint) && endPoint.length ! == 2 && (isOkey = false)
(point.constructor ! == Number) && (isOkey = false)
return isOkey
}
/* Parameter validation */
if (!Validityparameter()) {
return []
}
/* horizontal coordinates of point A */
const xA = 0
/* the vertical coordinate of point A */
const yA = 0
/* x-axis offset */
const offsetX = startPoint[0]
/* y-axis offset */
const offsetY = startPoint[1]
/* horizontal coordinate of point B */
const xB = endPoint[0] - offsetX
/* B vertical coordinate */
const yB = endPoint[1] - offsetY
/* coefficients a,b based on the coordinates of point B and the maximum height h */
let b = 0
let a = 0
/* Calculate the coefficients a ,b */
function handerComputer() {
if (h < 10) {
a = yB / Math.pow(xB, 2)
} else {
/* Since the general cart case is down, we actually have the cart coordinate system reversed, so we'll set h to a negative value here */
h = -h
/* Solve a,b quadratically, now knowing a point ( xB , yB ) another point (maxHx, h) */
/* the x coordinate when the highest point is effectively reached */
const effectMaHx = hclientX && Math.abs(hclientX - offsetX) > 0 && Math.abs(hclientX - offsetX) < Math.abs(xB)
/* If hclientX does not meet the requirement, then choose A , B midpoint as */
let maxHx = effectMaHx ? (hclientX - offsetX) : (xB + xA) / 2
/* We know the two points and find the values of a , b. Solve the equation to get y = ax^2 + bx */
a = ((yB / xB) - (h / maxHx)) / (xB - maxHx)
/* Bring a into one of the solutions b */
b = (yB - a * Math.pow(xB, 2)) / xB
}
}
/* Array of trajectories */
const travelList = []
/* x evenly divided */
const averageX = (xB - xA) / point
/* Handle linear motion */
function handerLinearMotion(type) {
if (type === 'X') {
const averageY = (yB - yA) / point
for (let i = 1; i <= point; i++) {
travelList.push([offsetX, i * averageY + offsetY])
}
} else {
for (let i = 1; i <= point; i++) {
travelList.push([offsetX + i * averageX, offsetY])
}
}
return travelList
}
/* When the absolute value of xB is less than 10, we treat it as a straight-line operation on the y-axis */
if (Math.abs(xB) < 10) {
return handerLinearMotion('X')
}
/* When the absolute value of yB is less than 10, we treat it as x-axis linear motion */
if (Math.abs(yB) < 10) {
return handerLinearMotion('Y')
}
handerComputer()
/* Draw the path */
for (let i = 1; i <= point; i++) {
const currentX = averageX * i
const currentY = Math.pow(currentX, 2) * a + b * currentX - yA
travelList.push([currentX + offsetX, currentY + offsetY])
}
return travelList
}
export default flycart
効果
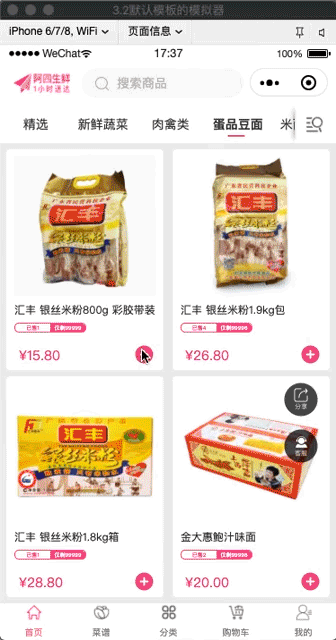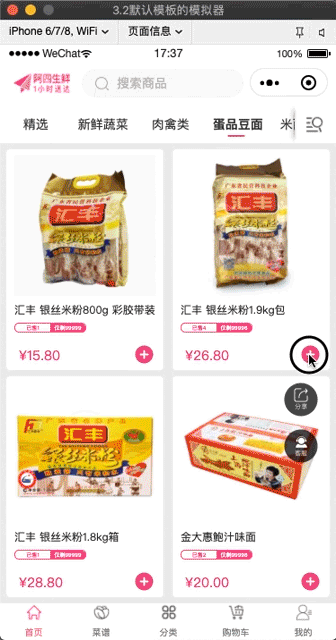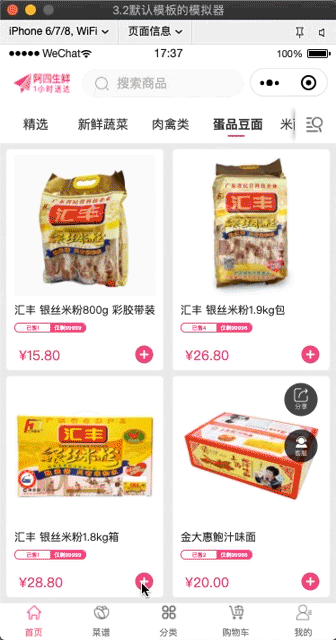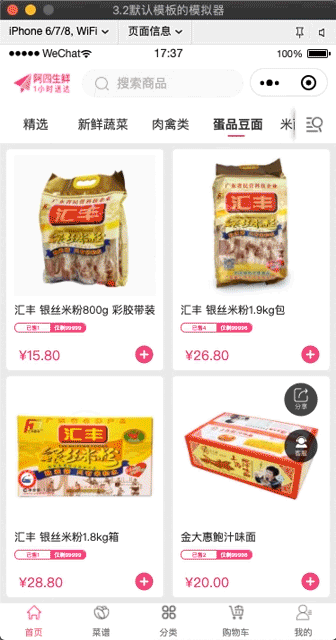
アプレットh5フライインカートコンポーネント?
ここでソリューションとコンポーネントをリンクさせれば、フライインショッピングカートコンポーネントの出来上がりです。
1このプログラムは、左の放物線ポイントを取得することです、トップ値は、我々はちょうど左の値のショッピングカートの絵に飛ぶ変更する必要があります,トップは2が拡大率を変更するには、カウンター機能を介して変更することができ、それを率直に言うと、画像の変換を変更することです:スケール値3ああ画像に固定位置を追加することを忘れないでください:笑顔:笑顔:メインデモ方法(参考用)::笑
startCart(){
/* open cart */
/* this.start stores the start point clientY clientY ,this.end stores the final point clientX clientY */
this.start = {}
this.start['x'] = this.data.current['x']
this.start['y'] = this.data.current['y']
const travelList = flycart([ this.start['x'] , this.start['y'] ] ,[ this.end['x'] , this.end['y'] ],25,50 )
this.startAnimate(travelList)
},
startAnimate(travelList) {
let index = 0
this.setData({
cartHidden: false,
bus_x: this.start['x'],
bus_y: this.start['y']
})
if(travelList.length=== 0) return
this.timer = setInterval( ()=> {
index++
const currentPoint = travelList.shift()
this.setData({
bus_x: currentPoint[0],
bus_y: currentPoint[1],
scale: 1 - index / 25
})
if (travelList.length === 0) {
clearInterval(this.timer)
this.triggerEvent('close')
}
}, 33)
}
ここでは ネイティブアプレットフライインカートコンポーネント h5はあまり変わりませんね。
gitのアドレスは以下の通りです。
コードのアドレス https://github.com/AlienZhaolin/flycart
この記事はhtml5アプレットフライインショッピングカート(放物線描画モーショントラックポイント)について紹介されています、より関連するhtml5フライインショッピングカートの内容は、スクリプトホーム以前の記事を検索するか、次の関連記事を閲覧を続けてください、あなたは将来的に多くのスクリプトホームをサポートして願っています!。
関連
-
Html5は、同時に複数のsdkのヒントをサポートする
-
画像のウォーターフォールレイアウトを実現するHTML+CSS+JSのサンプルコード
-
キャンバスは、ビデオの最初のサムネイルを取得します。
-
recorder.js Html5ベースの録画機能実装
-
iframeとwindow.onloadの詳しい使い方
-
クロスドメイン・モディフィケーション iframeページのコンテンツ詳細
-
タオバオH5サイン暗号化アルゴリズムの詳細
-
HD画面でのキャンバスサイズリセットによる不具合の解消について
-
HTML5新フォームコントロールとフォームプロパティのサンプルコード詳細
-
キャンバスでDVDスタンバイのアニメーションを作成するコード
最新
-
nginxです。[emerg] 0.0.0.0:80 への bind() に失敗しました (98: アドレスは既に使用中です)
-
htmlページでギリシャ文字を使うには
-
ピュアhtml+cssでの要素読み込み効果
-
純粋なhtml + cssで五輪を実現するサンプルコード
-
ナビゲーションバー・ドロップダウンメニューのHTML+CSSサンプルコード
-
タイピング効果を実現するピュアhtml+css
-
htmlの選択ボックスのプレースホルダー作成に関する質問
-
html css3 伸縮しない 画像表示効果
-
トップナビゲーションバーメニュー作成用HTML+CSS
-
html+css 実装 サイバーパンク風ボタン
おすすめ
-
Html5で新しくなったこと
-
HTMLスケッチのためのEmmet構文ルールの実装
-
HTML5+ API plusreadyの互換性問題について
-
HTML5でtitleタグに小さなアイコンを設定する方法
-
Html5 埋め込みピン留めサンプル実装
-
データストレージの3つの方法、Cookie sessionstorage localstorageの類似点と相違点の分析
-
iframeのクロスドメインでよく使われるいくつかの方法
-
カスタムお絵かきボード用JavaScript+Canvasサンプルコード
-
HTML5ページシームレス点滅オープン問題と解決策
-
ベッセル曲線の軌跡アニメーションのためのCanvasサンプルコード