最後に、こんなのもあります。 スニペット に関する Python ドキュメントからの .imap() のPythonドキュメントからのスニペットで、さらに私の好奇心を駆り立てます。

その chunksize という引数は map() メソッドと同じです。非常に長いイテラブルのために大きな値の chunksize は を使うことで 大いに をより速く完了させることができます。

_{関連する回答は参考になりますが、少しレベルが高すぎます。 Python のマルチプロセシング：なぜ大きなチャンクサイズは遅くなるのですか？ .}

どのように解決するのですか？

簡単な答え

Pool の chunksize-algorithm は発見的なものです。これは、Pool のメソッドに詰め込もうとしている、想像しうるすべての問題シナリオに対する簡単な解決策を提供するものです。その結果、どのような 特定の シナリオに最適化することはできません。

このアルゴリズムは、素朴なアプローチに比べて約4倍のチャンクで反復可能を任意に分割します。より多くのチャンクは、より多くのオーバーヘッドを意味しますが、スケジューリングの柔軟性は向上します。この回答が示すように、これは平均してより高いワーカー使用率につながりますが がなければ はなく、すべてのケースで全体の計算時間が短くなるという保証があります。

しかし、これを知ることが、具体的なマルチプロセシングの問題にどのように役立つのでしょうか。もっと正直に言うと、「短い答えはない」「マルチプロセシングは複雑だ」「場合による」ということです。観察された症状は、同じようなシナリオであっても、異なるルーツを持つことがあります。

この回答は、Pool のスケジューリング ブラックボックスをより明確に把握するのに役立つ基本的な概念を提供しようとするものです。また、チャンクサイズに関連する限り、潜在的な崖を認識し回避するための基本的なツールを提供しようとします。

目次

第一部

1. 定義
2. 並列化の目標
3. 並列化のシナリオ
4. チャンクサイズ 1 のリスク
5. プールのチャンクサイズアルゴリズム

6. アルゴリズムの効率性の定量化

   6.1モデル

   6.2 パラレルスケジュール

   6.3 効率の良さ

   6.3.1 絶対的な配電効率（ADE）

   6.3.2 相対分布効率(RDE)

第二部

1. NaiveとPoolのチャンクスサイズアルゴリズムの比較
2. リアリティチェック
3. 結論

まず、いくつかの重要な用語を明らかにしておく必要があります。

1. 定義

チャンク

ここでのチャンクは iterable -引数で指定されたプールメソッド呼び出しのシェアです。チャンクサイズがどのように計算されるのか、そしてどのような効果があるのか、それがこの回答のトピックです。

タスク

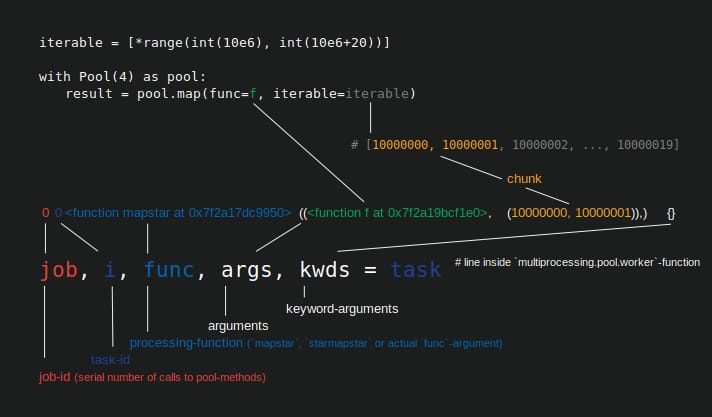
ワーカープロセスにおけるタスクの物理的なデータ表現は、下図のようになります。

図に示すのは pool.map() の呼び出しの例で、コードの行にそって表示されています。 multiprocessing.pool.worker 関数から読み込まれたタスクは inqueue から読み込まれたタスクは解凍されます。 worker はその基礎となる主関数で MainThread にあるプールワーカープロセスの そのため func -引数は、プールメソッドで指定された func -の中の変数にのみマッチします。 worker -のようなシングルコールのメソッドのための -function の中にあります。 apply_async と imap で chunksize=1 . 残りのプールメソッドには chunksize -パラメータを持つプールメソッドでは、処理関数 func はマッパー関数( mapstar または starmapstar ). この関数は、ユーザが指定した func -パラメータを、反復処理可能なチャンクの各要素にマッピングします (--> "map-tasks" )。この処理にかかる時間は タスク としても定義されます。 作業単位 .

タスケル

タスクという言葉が使われるようになったのは、そのためです。 全体 のコードと一致します。 multiprocessing.pool がどのように処理されるかは示されていません。 シングルコール をユーザが指定した func を、引数として のような、チャンクの1つの要素を引数として参照する必要があります。名前の衝突による混乱を避けるために（例えば maxtasksperchild -パラメータはプールの __init__ -メソッド) を使っている場合、この回答では、タスク内の単一の作業単位を タスク内の単一の作業単位を タスクル .

A タクセル から タスク＋エル ement)は、あるプロジェクトの中での仕事の最小単位です。 タスク . で指定された関数の単一の実行です。 func の - パラメータで指定された関数を実行します。 Pool -メソッドから得られた引数で呼び出されます。 単一の要素 送信された チャンク . A タスク で構成されます。 chunksize タスケル .

並列化オーバーヘッド(PO)

PO は、Python内部のオーバーヘッドとプロセス間通信（IPC）のオーバーヘッドから構成されています。Python内部のタスク単位のオーバーヘッドは、タスクとその結果をパッケージング、アンパックするために必要なコードに由来します。IPCオーバーヘッドは、スレッドの同期と異なるアドレス空間間でのデータのコピーに必要です（2つのコピーステップが必要：親 -> キュー -> 子）。IPC オーバーヘッドの量は、OS、ハードウェア、およびデータ サイズに依存するため、影響についての一般論は困難です。

2. 並列化の目標

マルチプロセシングを使用する場合、私たちの全体的な目標は（当然）すべてのタスクの総処理時間を最小化することです。この全体的な目標に到達するために、私たちの 技術的目標 である必要があります。 ハードウェアリソースの利用を最適化すること .

技術的な目標を達成するための重要な副目標をいくつか挙げます。

• 並列化オーバーヘッドを最小化する (最も有名ですが、それだけではありません。 IPC )
• すべての CPU コアの高い使用率
• OS が過剰なページングを行わないように、メモリ使用量を制限しておく ( トラッシング )

最初は、タスクは十分に計算量の多い（インテンシブ）ものである必要があります。 取り戻す を得るためには、並列化のために支払わなければなりません。PO の重要性は、タスクごとの絶対計算時間が長くなるほど低下します。逆に言えば、絶対的な計算時間が大きくなればなるほど、POは減少します。 タスクルごと の場合、POを削減する必要性は低くなります。もし、計算が1タスクあたり何時間もかかるのであれば、IPCのオーバーヘッドは無視できるほど小さくなります。ここでの主な関心事は、すべてのタスクが分散された後にワーカープロセスがアイドリングしないようにすることです。すべてのコアの負荷を維持することは、可能な限り並列化することを意味します。

3. 並列化シナリオ

multiprocessing.Pool.map() のようなメソッドへの最適なチャンクサイズの引数を決定する要因は何ですか？

問題となる主要な要因は、どの程度の計算時間が が変わるかです。 である。それを挙げると、最適なチャンクサイズの選択は 変動係数 ( CV ) を使って、タスクルあたりの計算時間を計算します。

このばらつきの大きさから、スケール上の2つの極端なシナリオは次のとおりです。

1. すべてのタスケルがまったく同じ計算時間を必要とする。
2. タスクエルは数秒で終わることもあれば、数日かかることもある。

覚えやすいように、これらのシナリオをこう呼ぶことにします。

1. 密なシナリオ
2. ワイドシナリオ

緻密なシナリオ

で 密なシナリオ では、必要な IPC とコンテキストスイッチを最小限に抑えるために、すべてのタスクセルを一度に配布することが望ましいと思われます。これは、ワーカープロセスの数だけチャンクを作成したいことを意味します。すでに述べたように、POの重みはタスクルごとの計算時間が短いほど増えます。

最大スループットのために、我々はまた、すべてのタスクが処理されるまで、すべてのワーカープロセスをビジーにしたい（アイドリングワーカーなし）。この目標のために、分散されたチャンクは等しいサイズかそれに近いものであるべきです。

ワイドシナリオ

の代表的な例です。 ワイドシナリオ の典型的な例は、結果がすぐに収束するか、計算が何日もかかるような最適化問題でしょう。通常、このような場合、タスクにどのような軽いタスクと重いタスクが混在しているかは予測できません。一度に配布するタスクの数をできるだけ少なくすることは、スケジューリングの柔軟性を高めることを意味します。これは、すべてのコアを高稼働させるという副目標を達成するために必要です。

もし Pool メソッドがデフォルトで Dense シナリオに完全に最適化されている場合、Wide シナリオに近い位置にあるすべての問題に対して最適でないタイミングを作成することが多くなります。

4. チャンクスサイズのリスク > 1

この単純化された疑似コードの例について考えてみましょう。 ワイドシナリオ -これは pool-method に渡したいものです。

good_luck_iterable = [60, 60, 86400, 60, 86400, 60, 60, 84600]

実際の値の代わりに、必要な計算時間を秒単位で、簡単のために1分または1日だけ表示するようにします。 プールには4つのワーカープロセス（4つのコア上）があると仮定します。 chunksize に設定されています。 2 . 順序が保たれるので、ワーカーに送られるチャンクはこれらになります。

[(60, 60), (86400, 60), (86400, 60), (60, 84600)]

十分な数のワーカーがいて、計算時間が十分に長いので、すべてのワーカープロセスは最初に作業するチャンクを得ることができると言えます。(これは高速に完了するタスクの場合である必要はありません)。さらに、全体の処理には約 86400+60 秒かかると言えます。これは、この人工的なシナリオにおけるチャンクの総計算時間が最も長く、チャンクを 1 回だけ配布するためです。

ここで、前の反復可能性と比べて位置を変える要素が1つしかない、この反復可能性を考えてみましょう。

bad_luck_iterable = [60, 60, 86400, 86400, 60, 60, 60, 84600]

...そして対応するチャンク

[(60, 60), (86400, 86400), (60, 60), (60, 84600)]

イテラブルのソートで運が悪かっただけで、総処理時間はほぼ2倍 (86400+86400) になってしまいました! 悪質な (86400, 86400) チャンクを取得したワーカーは、そのタスクの 2 番目の重いタスクが、すでに (60, 60) チャンクを終えたアイドリング中のワーカーの 1 人に分配されるのをブロックしているのです。を設定すれば、このような不愉快な結果を招く危険はないことは明らかです。 chunksize=1 .

これはより大きなチャンクサイズのリスクです。チャンクサイズを大きくすることで、スケジューリングの柔軟性とオーバーヘッドの削減を交換することになりますが、上記のようなケースでは、これは悪い取り引きです。

章ではどのように見るか 6. アルゴリズム効率の定量化 において、より大きなチャンクサイズは最適でない結果につながることもあります。 密なシナリオ .

5. プールのチャンクスサイズアルゴリズム

以下に、ソース コード内のアルゴリズムを少し修正したものを示します。ご覧のように、私は下の部分を切り落とし、それを chunksize 引数を外部で計算するための関数にラップしました。また 4 を factor パラメータを付けてアウトソースし len() の呼び出しをアウトソースしています。

# mp_utils.py

def calc_chunksize(n_workers, len_iterable, factor=4):
    """Calculate chunksize argument for Pool-methods.

    Resembles source-code within `multiprocessing.pool.Pool._map_async`.
    """
    chunksize, extra = divmod(len_iterable, n_workers * factor)
    if extra:
        chunksize += 1
    return chunksize

全員が同じページにいることを確認するために、以下は divmod が行うことを説明します。

divmod(x, y) は組み込み関数で (x//y, x%y) . x // y は床分割で x / y であるのに対し x % y から余りを返すモジュロ演算です。 x / y . したがって，例えば divmod(10, 3) は (3, 1) .

ここで chunksize, extra = divmod(len_iterable, n_workers * 4) を見てみると n_workers は除数です。 y で x / y との乗算は 4 によって、さらに調整することなく if extra: chunksize +=1 で調整することなく、初期チャンクサイズを は少なくとも の4倍小さくなります( len_iterable >= n_workers * 4 の場合)、そうでない場合よりも4倍小さくなります。

による乗算の効果を見るために 4 による乗算の効果を見るには、この関数を検討してください。

def compare_chunksizes(len_iterable, n_workers=4):
    """Calculate naive chunksize, Pool's stage-1 chunksize and the chunksize
    for Pool's complete algorithm. Return chunksizes and the real factors by
    which naive chunksizes are bigger.
    """
    cs_naive = len_iterable // n_workers or 1  # naive approach
    cs_pool1 = len_iterable // (n_workers * 4) or 1  # incomplete pool algo.
    cs_pool2 = calc_chunksize(n_workers, len_iterable)

    real_factor_pool1 = cs_naive / cs_pool1
    real_factor_pool2 = cs_naive / cs_pool2

    return cs_naive, cs_pool1, cs_pool2, real_factor_pool1, real_factor_pool2

上の関数は、素朴なチャンクサイズを計算します ( cs_naive ) と、Pool のチャンクサイズアルゴリズムの最初のステップのチャンクサイズ ( cs_pool1 )、そして完全な Pool-algorithm のチャンクサイズ ( cs_pool2 ). さらに 実係数 rf_pool1 = cs_naive / cs_pool1 そして rf_pool2 = cs_naive / cs_pool2 これは、単純に計算されたチャンクサイズが、プールの内部バージョンより何倍大きいかを教えてくれます。

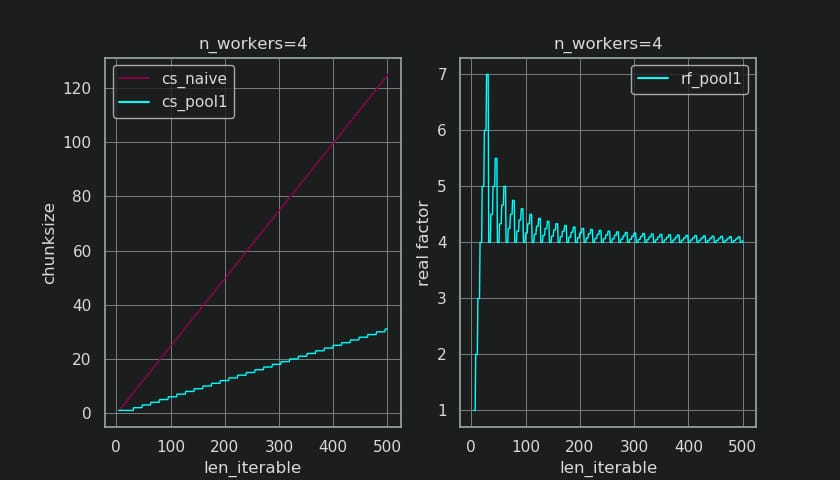
この関数の出力で作成された 2 つの図を以下に示します。左の図は、単に n_workers=4 の反復可能な長さまでの 500 . 右図は rf_pool1 . 反復可能な長さに対して 16 の場合、実係数は >=4 (この場合 len_iterable >= n_workers * 4 ) であり、その最大値は 7 反復可能な長さに対して 28-31 . これは、元の要因から大きく逸脱しています。 4 に収束してしまいます。ここでの「より長い」は相対的なもので、指定されたワーカーの数に依存します。

チャンクサイズを記憶する cs_pool1 にはまだ extra -からの残りで調整されます。 divmod に含まれる cs_pool2 は完全なアルゴリズムから

とアルゴリズムが進みます。

if extra:
    chunksize += 1

今度は は がある場合、余分な extra divmod-operation から）、チャンクサイズを 1 増やすことは、明らかにすべてのタスクでうまくいくわけではありません。結局のところ、もしそうであれば、そもそも余りはないでしょう。

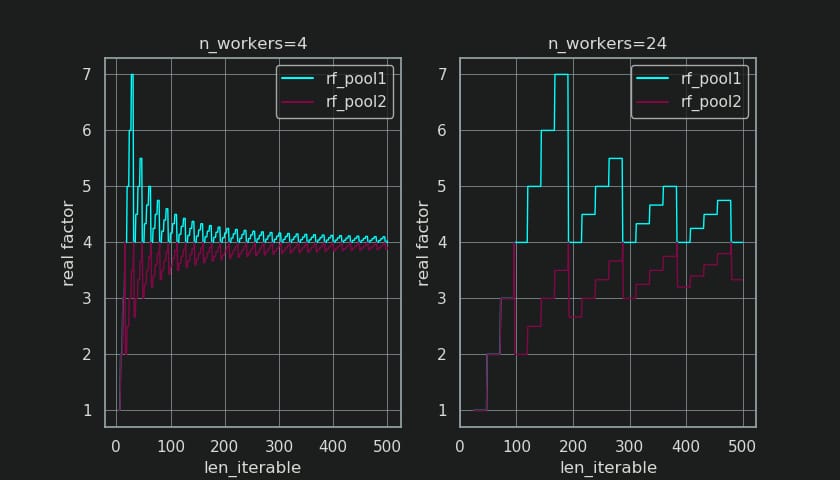
下の図でわかるように、quot; 余分な処理 "は、その効果として 実因子 については rf_pool2 に収束するようになりました。 4 から 以下 4 となっており、偏差がやや滑らかになっています。の標準偏差は n_workers=4 と len_iterable=500 からドロップします。 0.5233 に対して rf_pool1 に 0.4115 に対して rf_pool2 .

最終的に、増加する chunksize を 1 つ増やすと、最後に転送されるタスクのサイズが len_iterable % chunksize or chunksize .

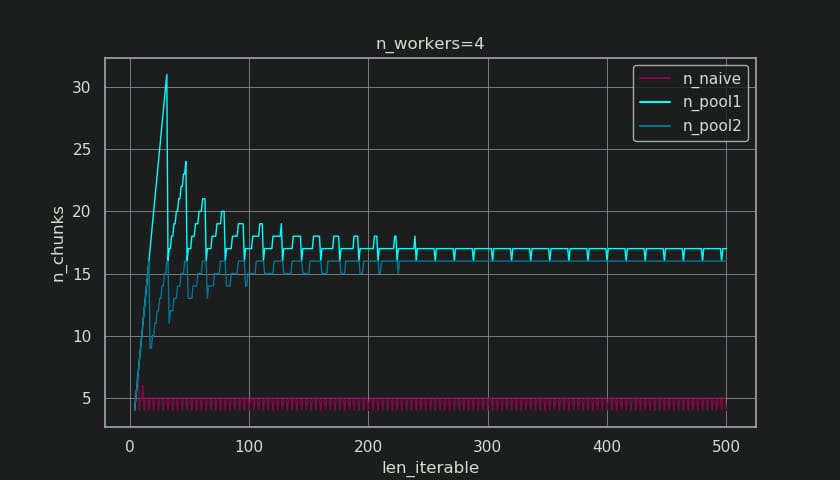
の、より興味深い、そしてどのように後で見るか、より結果的な、効果について。 追加治療 について観察することができます。 生成チャンクの数 ( n_chunks ). 十分長いイテラブルに対しては、プールが完成させたチャンクサイズアルゴリズム ( n_pool2 で安定化する。 n_chunks == n_workers * 4 . これに対して、素朴なアルゴリズムでは、(最初のバープの後) チャンク数を の間で交互に繰り返します。 n_chunks == n_workers と n_chunks == n_workers + 1 というように、反復可能な長さが長くなっていく。

以下に、プールと素朴なチャンクサイズアルゴリズムのために拡張された2つの情報関数を紹介します。これらの関数の出力は、次の章で必要になります。

# mp_utils.py

from collections import namedtuple


Chunkinfo = namedtuple(
    'Chunkinfo', ['n_workers', 'len_iterable', 'n_chunks',
                  'chunksize', 'last_chunk']
)

def calc_chunksize_info(n_workers, len_iterable, factor=4):
    """Calculate chunksize numbers."""
    chunksize, extra = divmod(len_iterable, n_workers * factor)
    if extra:
        chunksize += 1
    # `+ (len_iterable % chunksize > 0)` exploits that `True == 1`
    n_chunks = len_iterable // chunksize + (len_iterable % chunksize > 0)
    # exploit `0 == False`
    last_chunk = len_iterable % chunksize or chunksize

    return Chunkinfo(
        n_workers, len_iterable, n_chunks, chunksize, last_chunk
    )

のおそらく予想外の外観に惑わされないでください。 calc_naive_chunksize_info . その extra から divmod はチャンクサイズの計算には使用されません。

def calc_naive_chunksize_info(n_workers, len_iterable):
    """Calculate naive chunksize numbers."""
    chunksize, extra = divmod(len_iterable, n_workers)
    if chunksize == 0:
        chunksize = 1
        n_chunks = extra
        last_chunk = chunksize
    else:
        n_chunks = len_iterable // chunksize + (len_iterable % chunksize > 0)
        last_chunk = len_iterable % chunksize or chunksize

    return Chunkinfo(
        n_workers, len_iterable, n_chunks, chunksize, last_chunk
    )

6. アルゴリズム効率の定量化

の出力がどのようなものであるかを見てきました。 Pool のチャンクサイズアルゴリズムの出力が、素朴なアルゴリズムからの出力と比較してどのように違って見えるかを見てみましょう...。

• プールのアプローチが実際に 改善されるかどうか を向上させるのか？
• そして、これは一体何なのでしょうか？ 何か は何でしょうか？

前章で示したように、長いイテレート（タスクルの数が多い）場合、Poolのチャンクサイズアルゴリズムは はおよそ は反復表を 4 回に分割し より チャンクに分割します。小さなチャンクはより多くのタスクを意味し、より多くのタスクはより多くの 並列化オーバーヘッド(PO) これはスケジューリングの柔軟性を高めるという利点と比較検討されなければならないコストです (以下はその例です)。 "Risks of Chunksize>1" ).

かなり明白な理由により、Pool の基本的なチャンクサイズアルゴリズムは、スケジューリングの柔軟性と次のようなものを比較検討することができません。 PO を量ることができません。IPC-overhead は OS、ハードウェア、およびデータ サイズに依存します。アルゴリズムは、私たちがどのハードウェアでコードを実行するか知ることはできませんし、タスクルが終了するのにかかる時間の手がかりも持っていません。このアルゴリズムは すべて 基本的な機能を提供するヒューリスティックなものです。つまり、特定のシナリオのために最適化することはできません。前述したように PO もタスクルあたりの計算時間が長くなるにつれて、次第に気にならなくなります (負の相関)。

を思い出すと 並列化の目標 を第2章から思い出すと、一つの箇条書きがありました。

• すべての CPU コアで高い使用率

先に述べた 何か は、Pool のチャンクサイズアルゴリズムである は を改善しようとするのは アイドリング作業工程の最小化 であり、それぞれ CPUコアの利用率 .

に関するSOでの繰り返しの質問です。 multiprocessing.Pool に関する SO での繰り返しの質問は、すべてのワーカー プロセスがビジー状態であると予想される状況で、未使用のコアやアイドル状態のワーカー プロセスについて疑問に思う人々によって尋ねられたものです。これには多くの理由がありますが、計算の終わりに向かってアイドル状態のワーカー プロセッサを観察することは、たとえ 密なシナリオ (タスクルあたりの計算時間が等しい) 場合でも、ワーカー数が 除数 がチャンク数の n_chunks % n_workers > 0 ).

今問題になっているのは

チャンクサイズの理解を、観測されたワーカーの使用率を説明したり、その点で異なるアルゴリズムの効率を比較したりすることを可能にするものに、どのように実用的に変換できるでしょうか？

6.1 モデル

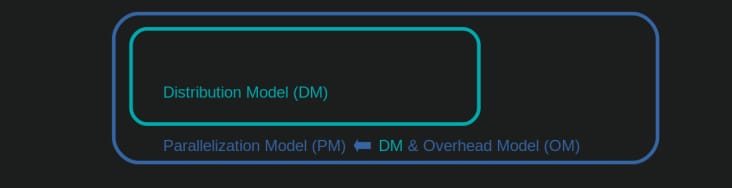
ここでより深い洞察を得るためには、定義された境界内で重要性を維持しながら、過度に複雑な現実を管理可能な程度まで単純化する、並列計算の抽象化の形式が必要です。このような抽象化は モデル . このような"の実装は 並列化モデル" (PM) は、実際の計算と同じようにワーカーマップされたメタデータ（タイムスタンプ）を生成します。このモデルによって生成されたメタデータを用いることで、ある制約のもとでの並列計算の指標を予測することができます。

ここで定義された PM は ディストリビューションモデル(DM) . は DM は、仕事の原子単位（タスクル）が、どのように 並列作業者と時間 を説明します。それぞれのチャンクサイズアルゴリズム、ワーカーの数、入力反復子（taskelの数）、およびそれらの計算時間以外の要因が考慮されない場合です。つまり、あらゆる形式のオーバーヘッドが ではなく は含まれないということです。

完全な PM を得るためには DM が拡張され オーバーヘッドモデル(OM) の様々な形式を表現します。 並列化オーバーヘッド(PO) . このようなモデルは、各ノードに対して個別にキャリブレーションする必要があります（ハードウェア、OSへの依存）。オーバーヘッドがいくつの形式で表現されるかは OM はオープンなままなので、複数の OM が存在しうる。実装されたOMがどの程度の精度を持つか OM の全体的な重みによって決定されます。 PO の全体的な重みで決まります。タスクルが短ければ短いほど PO の比重が高くなり、その結果、より正確な OM を行おうとしているのであれば を予測する 並列化効率(PE) .

6.2 パラレルスケジュール(PS)

は 並列スケジュール は並列計算の2次元表現で、X軸は時間、Y軸は並列作業者のプールを表します。ワーカーの数と総計算時間は長方形の延長を示し、その中に小さな長方形が描かれています。これらの小さい長方形は仕事の原子単位（タスクル）を表しています。

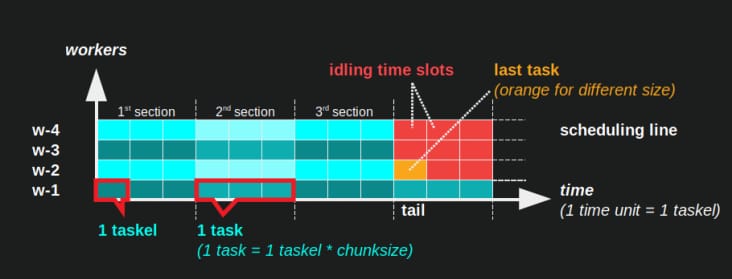
の視覚化を以下に示します。 PS のデータで描かれた DM のための Pool のチャンクサイズアルゴリズムのデータです。 密なシナリオ .

• x 軸は時間の等しい単位に分割され、各単位はタスクルが必要とする計算時間を表します。
• y 軸は、プールが使用するワーカー・プロセスの数に分割されます。
• ここでのタスクルは、匿名化されたワーカープロセスのタイムライン (スケジュール) に入れられた、最小のシアン色の四角形として表示されます。
• タスクは、ワーカータイムラインの 1 つまたは複数のタスクで、同じ色で連続的にハイライトされます。
• アイドリング時間単位は、赤色のタイルで表現されます。
• Parallel Scheduleはセクションに分割されています。最後のセクションはテールセクションである。

構成された部分の名称は下図のようになる。

完全な PM を含む OM は、その アイドリング・シェア は、テールだけでなく、タスクとタスクの間、さらにはタスクとタスクの間にも存在する。

6.3 効率性

上で紹介したモデルによって、労働者の利用率を定量化することができます。区別することができる。

• ディストリビューション効率 (DE) - の助けを借りて計算されます。 DM (の簡便法）。 デンスシナリオ ).
• 並列化効率(PE) - 較正された PM (予測)の助けを借りて計算されたもの、または実際の計算のメタデータから計算されたものです。

重要なのは、計算された効率は はありません。 と自動的に関連付けられます。 より速く と自動的に相関します。この文脈でのワーカーの使用は、開始済みで未完了のタスクルを持つワーカーと、そのようなオープンなタスクルを持たないワーカーを区別するだけです。つまり、アイドリングの可能性がある 期間中 タスクのタイムスパンは ではなく が登録されています。

上記の効率はすべて、基本的に除算の商を計算することによって得られるものである ビジーシェア・並行スケジュール . との差は デ と PE は、ビジー・シェアが付きます。 は、オーバーヘッドを伸ばした分、並列スケジュール全体の中でより小さな部分を占めます。 PM .

この回答では、さらに、簡単な計算方法についてだけ説明します。 DE を計算する簡単な方法についてのみ説明します。これは異なるチャンクサイズアルゴリズムを比較するのに十分であり、なぜなら...

1. ... DM の部分は PM の部分であり、採用するチャンクサイズアルゴリズムの違いで変化します。
2. ... Dense シナリオ で、タスクルごとの計算時間が等しい場合、これらの時間スパンが方程式から脱落する安定状態を描きます。他のシナリオでは、タスクルの順序が重要であるため、ランダムな結果になるだけです。

6.3.1 絶対分布効率 (ADE)

この基本的な効率は、一般的には ビジーシェア の全電位を通して計算することができます。 並行スケジュール :

絶対分布効率(ADE) = ビジー・シェア / 並行スケジュール

については 密なシナリオ では、簡略化した計算コードは次のようになります。

# mp_utils.py

def calc_ade(n_workers, len_iterable, n_chunks, chunksize, last_chunk):
    """Calculate Absolute Distribution Efficiency (ADE).

    `len_iterable` is not used, but contained to keep a consistent signature
    with `calc_rde`.
    """
    if n_workers == 1:
        return 1

    potential = (
        ((n_chunks // n_workers + (n_chunks % n_workers > 1)) * chunksize)
        + (n_chunks % n_workers == 1) * last_chunk
    ) * n_workers

    n_full_chunks = n_chunks - (chunksize > last_chunk)
    taskels_in_regular_chunks = n_full_chunks * chunksize
    real = taskels_in_regular_chunks + (chunksize > last_chunk) * last_chunk
    ade = real / potential

    return ade

がない場合は アイドリング・シェア , ビジー・シェア になります。 等しい になります。 並行スケジュール であり、それゆえ ADE は100%になります。この単純化されたモデルでは、すべてのタスクの処理に必要な時間を通して、利用可能なすべてのプロセスがビジー状態であるシナリオです。言い換えると、ジョブ全体が 100 % の並列化を効果的に行うことができます。

しかし、なぜ私は PE として 絶対 PE ここで？

それを理解するために、スケジューリングの柔軟性を最大化するチャンクサイズ（cs）の可能なケースを考える必要があります（また、ハイランダーが存在できる数。 偶然でしょうか）。

__________________________________ ~ ONE __________________________________

例えば、4 つのワーカープロセスと 37 個のタスクがある場合、次のようにしてもアイドリングワーカーが存在します。 chunksize=1 という理由で n_workers=4 は37の約数ではないので 37 / 4を割った余りは1です。この1つの残りのタスクは、1人の作業者が処理しなければならず、残りの3人はアイドリング状態になっています。

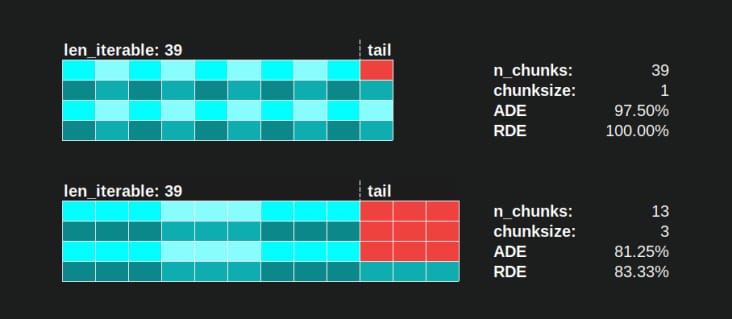
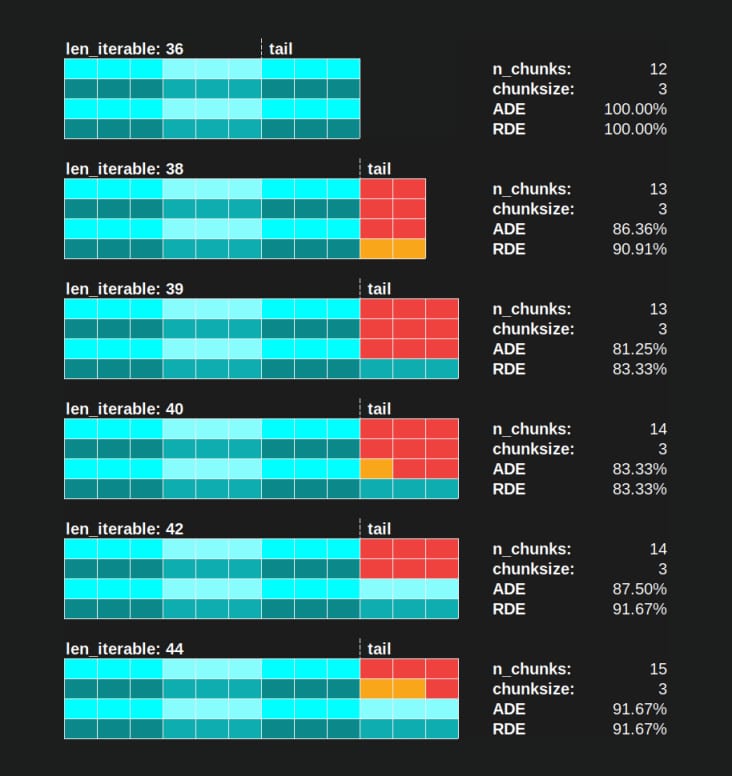
同様に、39個のタスキを持つアイドリング状態の作業者が1人残ることになりますが、これは以下の写真のようになります。

上段と下段を比較すると 並列スケジュール に対して chunksize=1 に対して、以下のバージョンで chunksize=3 の場合、上の 並列スケジュール が小さくなり、X 軸のタイムラインは短くなっています。これで、より大きなチャンクサイズが、意外にも が の場合でも、全体的な計算時間の増加につながることがわかります。 密なシナリオ .

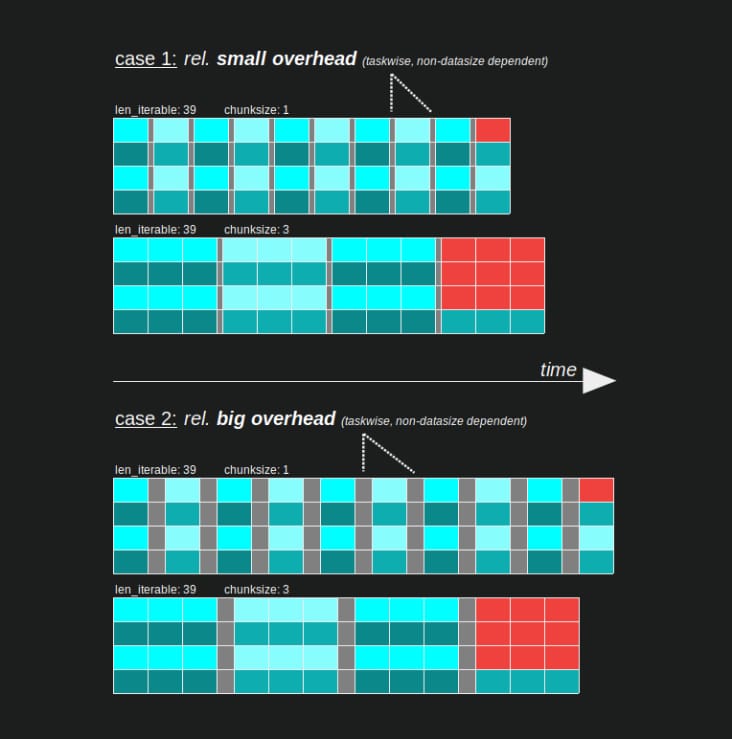
でも、効率計算にはX軸の長さだけでいいのでは？

なぜなら、オーバーヘッドはこのモデルには含まれないからです。オーバーヘッドは両方のチャンクサイズで異なるため、x 軸は実際には直接比較できません。オーバーヘッドがあると、次のように総計算時間が長くなる可能性があります。 ケース 2 のように計算時間が長くなることがあります。

6.3.2 相対分布効率 (RDE)

は ADE の値には、もし より良い チャンクサイズを1に設定すると、タスクの分配が可能になります。 より良い というのは、この場合でも、より小さい アイドリング・シェア .

を取得するために DE の値が最大になるように調整された DE を分割する必要があります。 ADE を通して ADE で得られる chunksize=1 .

相対分布効率(RDE) = ADE_cs_x / ADE_cs_1

コードで見るとこんな感じです。

# mp_utils.py

def calc_rde(n_workers, len_iterable, n_chunks, chunksize, last_chunk):
    """Calculate Relative Distribution Efficiency (RDE)."""
    ade_cs1 = calc_ade(
        n_workers, len_iterable, n_chunks=len_iterable,
        chunksize=1, last_chunk=1
    )
    ade = calc_ade(n_workers, len_iterable, n_chunks, chunksize, last_chunk)
    rde = ade / ade_cs1

    return rde

RDE の尻尾の話であり、ここで定義された方法は、要するに パラレル・スケジュール . RDE は、テールに含まれる最大有効チャンクサイズに影響されます。(このテールは x 軸の長さ chunksize または last_chunk .) これは、結果として RDE は自然に100%(偶数)に収束します。

低い RDE ...

• は、最適化の可能性を示す強いヒントです。
• の相対的な末尾の割合が大きくなるため、長い反復記号では当然可能性が低くなります。 並列スケジュール が縮まるからです。

この回答のパート II を参照してください。 ここで .