2019年にこの記事を投稿し、これまで多くのご指摘をいただきました。当時は確かにコードが不明瞭でわかりにくかったので、最近時間ができたのでコードを整理し、ここに再送信しました。これで理解が深まれば幸いです。

モデリングの手順

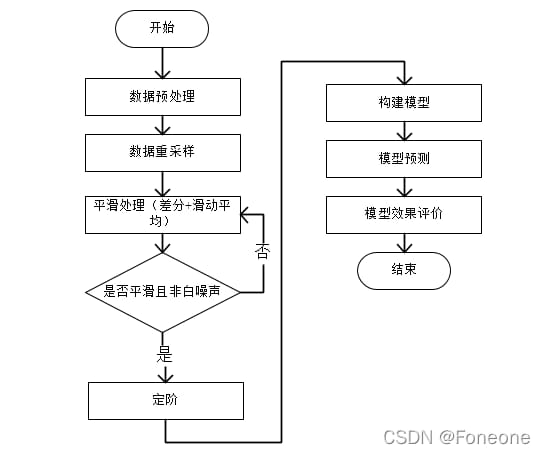
ディレクトリ

パケットとバージョンのアサーション

ステップ1：データの準備とデータの前処理

ステップ2：データ再サンプリング

ステップ3：平滑化

ステップ4：平滑化テスト

 ステップ5：時系列固定順序

(2) 情報量規準のサイジング

ステップ6：モデルの構築

ステップ7：モデルの評価

概要

---

パケットとバージョンのアサーション

アファメーションです。この実験環境は python 3.7.4 statsmodels version: 0.10.1 です。

import pandas as pd 
import numpy as np
import seaborn as sns # heat map
import itertools 
import datetime
import matplotlib.pyplot as plt #draw a graph
import statsmodels.api as sm 
from sklearn.metrics import mean_squared_error
from statsmodels.tsa.stattools import adfuller #ADF test
from statsmodels.stats.diagnostic import acorr_ljungbox #white noise test
from statsmodels.graphics.tsaplots import plot_acf,plot_pacf #plot fixed order
from statsmodels.tsa.arima_model import ARIMA #ARIMA model
from statsmodels.tsa.arima_model import ARMA #ARMA model
from statsmodels.stats.stats.stattools import durbin_watson #DW test
from statsmodels.graphics.api import qqplot #qqplot

ステップ1：データの準備とデータの前処理

    標準正規分布に従う2018年1月1日から2018年9月1日までのデータを自動生成し、old_data.csvに格納する。

#### Part:generate raw data and save in the old_data.csv 
#### Create a time list from 20180101 to 20180901 data and save in the old_data.csv 
def genertate_data():
    index = pd.date_range(start='2018-1-1',end = '2018-9-1',freq='10T') # 10 minute sampling
    index = list(index)
    data_list = []
    for i in range(len(index)): 
        data_list.append(np.random.randn()) # data is a sample that fits the standard normal distribution
    dataframe = pd.DataFrame({'time':index,'values':data_list})
    dataframe.to_csv('G:\\WX\\2\\\old_data.csv',index=0)
    print('the data is existting')

私は、フォルダ内のいくつかの値をわざと-10000に変更して、例外にしました。（先生が、最後に高得点を取るためには、ステップをできるだけ完全に見せるようにと言ったので、自分で手作業で例外を追加しました）。この作品の主な作業は、pandasの中の関数を使って、単に 特殊な操作の後 データです。

#### Step 1 Data preprocessing
#### delete or revise some values in data and make data preprocessing
#### Delete or revise the created data and make data preprocessing 
def data_preprocessing():
    data = pd.read_csv('G:\\WX\\2\\\old_data.csv')
    #print(data.describe()) #check the statistics, find the minimum value of -10000 abnormal data
    #print((data.isnull()).sum()) #check if there are missing values
    #print((data.duplicated()).sum()) # Duplicate values
    def change_zero(x):
        if x == -10000:
            return 0
        else :
            return x
    data['values'] = data['values'].apply(lambda x: change_zero(x))
 
    # Fill in the missing values using the mean
    mean = data['values'].mean()
    def change_mean(x):
        if x == 0:
            return mean
        else:
            return x
    data['values'] = data['values'].apply(lambda x: change_mean(x))
    # Save the processed data
    data.to_csv('G:\\WX\\2\\\\new_data.csv',index=0)
    print('new data is existing')

ステップ2：データの再サンプリング

高いスコアを出すために（-、-）、多くのデータを行い、次に合計34,992のデータを持ち、そして少しリサンプリングを行い、そしてデータは数日でリサンプリングされました。

#### Step 2 Resample
#### Resample Data and Sampling frequency is days
#### Resampling, replacing the sampling frequency with days
def Resampling(): # resample
    df = pd.read_csv('G:\\WX\\2\\\new_data.csv')
     # Convert the default indexing method to time indexing
    df['time'] = pd.to_datetime(df['time'])
    df.set_index("time", inplace=True)
   
    train_data = df['2018-1-1':'2018-8-1'] ## fetch to 20180101 to 20180801 for training 
    test = df['2018-8-1':'2018-9-1'] ## fetch 20180801 to 20180901 for prediction 
    train_data = train_data.resample('D').mean() ## take the mean value in days, resample
    test_data = test.resample('D').mean()
 
    return train_data,test_data

ステップ3：スムージング

ARMAやARIMAでは、時系列が平滑性や非白色ノイズの要件を満たす必要があるため、差分と平滑化（ローリング平均とローリング標準偏差）を用いて時系列の平滑化操作を実現する。一般に、系列の平滑性を得るためには、時系列に対する1次差分法で十分であり、2次差分が必要な場合もある。

#### Step 3 Differentiation to smoothing
def stationarity(timeseries): # smoothing (timeseries time series)
    ## Differentiation, save as a new column
    diff1 = timeseries.diff(1).dropna() # 1st order differencing dropna() remove missing values
    diff2 = diff1.diff(1) # Do another first-order diff on top of the first-order diff, i.e. second-order dropna
    ## Plot
    #diff1.plot(color = 'red',title='diff 1',figsize=(10,4))
    #diff2.plot(color = 'black',title='diff 2',figsize=(10,4))

    
    ## Smoothing method
    rollmean = timeseries.rolling(window=4,center = False).mean() ## roll mean
    rollstd = timeseries.rolling(window=4,center = False).std() ## Roll standard deviation
    ## Plot 
    ## rollmean.plot(color = 'yellow',title='Rolling Mean',figsize=(10,4))
    #rollstd.plot(color = 'blue',title='Rolling Std',figsize=(10,4))
    
    return diff1,diff2,rollmean,rollstd

差分法の結果をプロットしたもの。このプロットから、一階差分法は基本的に平滑性の必要性を満たしていることがわかる。

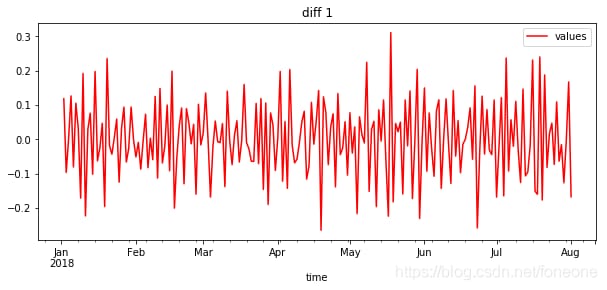
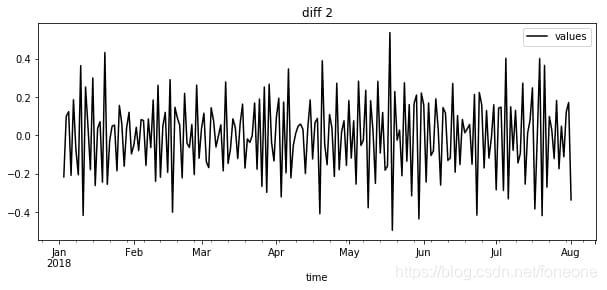
平滑化した結果を図に示します。

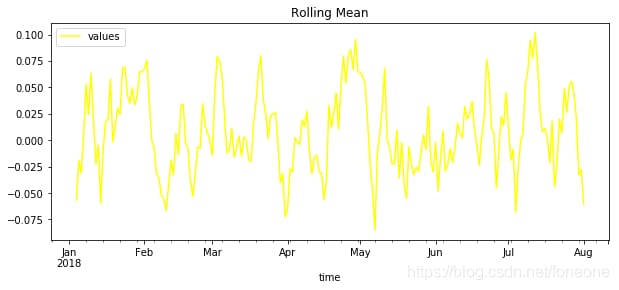
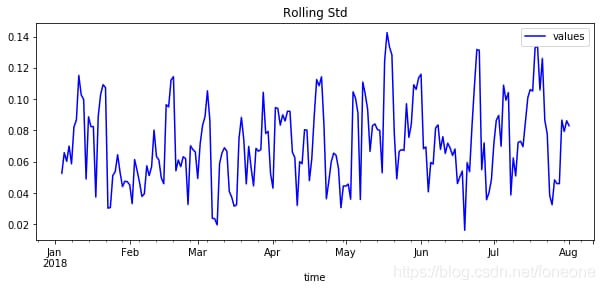
ご覧のように、私が作成したデータには、平滑化手法は全く合っていません。一般的には 平滑化法は、周期的な定常上昇をするデータ型に適している .

ステップ4：平滑性テスト

系列が滑らかかどうかを判断するにはADF検定を、系列がランダムかどうかを判断するには白色ノイズ検定を使用します。

#### Step 4 Smoothness test
def ADF_test(timeseries): ## Test for smoothness of the series
    x = np.array(timeseries['values'])
    adftest = adfuller(x, autolag='AIC')
    #print (adftest) 
    if adftest[0] < adftest[4]["1%"] and adftest[1] < 10**(-8): 
    # Compare Adf results with hypothesis test at 10% and whether P-value is very close to 0 (smaller is better)
        print("series is smooth")
        return True 
    else:
        print("non-stationary series")
        return False

def random_test(timeseries) : # randomness test (white noise test)
    p_value = acorr_ljungbox(timeseries, lags=1) # p_value returns a two-dimensional array, with the second dimension being the p-value
    if p_value[1] < 0.05: 
        print("non-randomness sequence")
        return True
    else:
        print("random sequence, i.e. white noise sequence")
        return False

(1) ADF 検定の結果は次のとおりである。

シーケンスがスムーズにできるかどうかは、どのように判断するのですか？主に見ることで。

(1) 原仮説の棄却水準が異なる場合の1%、%5、%10の統計値とADF検定の結果の比較。ADF検定の結果は、1％、5％、10％を同時に下回っており、仮説が非常によく棄却されていることがわかる。

(2) P 値が 0 に非常に近いかどうか このデータでは、P 値は 7.9e-10 であり、0 に近いと言える。

ADFの結果の見方については、こちらのブログ記事を参照してください。

ADFテストにおけるPython時系列詳細_学渣- CSDN博客_python for adf test

(2)ホワイトノイズの結果を図に示します。

統計量のP値が有意水準0.05より小さければ、信頼水準95%で原仮説を棄却でき、系列は非白色ノイズとみなされる（そうでなければ、原仮説が受け入れられ、系列は純粋にランダムとみなされる）。         

p値は0.315で0.05よりはるかに大きいので、時系列は白色雑音である、すなわち、時間相関のないランダムに生成された系列であるという原仮説を受け入れましょう。(教師がデータを与えなかったので、難しいが非白色ノイズと仮定しなければならないことを説明しなさい)

 ステップ5：時系列固定次数

オーダーフィックスには、大きく分けて2つの方法があります。

(1) ACFとPACFは、トレーリングテールとトランケートテールを使って

(2) 順序を決定するための情報量規準（AIC、BIC、HQIC）

ヒートマップは、pとqの値をより明示的に可視化するための補助的な手法であり、実はこれでも方法2「情報量規準の順序」である。

def determinate_order_acf(timeseries): # Use ACF and PACF to determine the model order 
    plot_acf(timeseries,lags=40) # number of delays
    plot_pacf(timeseries,lags=40)
    plt.show()
     
def detetminante_order_AIC(timeseries): #Information criterion for fixing order: AIC, BIC, HQIC
    #AIC
    AIC = sm.tsa.arma_order_select_ic(timeseries,\
        max_ar=6,max_ma=4,ic='aic')['aic_min_order']
    #BIC
    BIC = sm.tsa.arma_order_select_ic(timeseries,max_ar=6,\
           max_ma=4,ic='bic')['bic_min_order']
    #HQIC
    HQIC = sm.tsa.arma_order_select_ic(timeseries,max_ar=6,\
                 max_ma=4,ic='hqic')['hqic_min_order']
    print('the AIC is{},\nthe BIC is{}\n the HQIC is{}'.format(AIC,BIC,HQIC))

def heatmap_AIC(timeseries):
    # Set the initial conditions of the traversal loop, displayed as a heat map, same principle as AIC, BIC, HQIC fixed order
    p_min = 0
    q_min = 0
    p_max = 5
    q_max = 5
    d_min = 0
    d_max = 5
    # Create Dataframe, with BIC criteria
    results_aic = pd.DataFrame(index=['AR{}'.format(i)\
                               for i in range(p_min,p_max+1)],\
            columns=['MA{}'.format(i) for i in range(q_min,q_max+1)])
    # itertools.product returns a tuple of Cartesian products of the elements in p,q
    for p,d,q in itertools.product(range(p_min,p_max+1),\
                                   range(d_min,d_max+1),range(q_min,q_max+1)):
        if p==0 and q==0:
            results_aic.loc['AR{}'.format(p), 'MA{}'.format(q)] = np.nan
            continue
        try:
            model = sm.tsa.ARIMA(timeseries, order=(p, d, q))
            results = model.fit()
            # return the BIC value of the model for different pq
            results_aic.loc['AR{}'.format(p), 'MA{}'.format(q)] = results.aic
        except:
            continue
    results_aic = results_aic[results_aic.columns].astype(float)
    #print(results_bic)
    
    fig, ax = plt.subplots(figsize=(10, 8))
    ax = sns.heatmap(results_aic,
                 #mask=results_aic.isnull(),
                 ax=ax,
                 annot=True, # display the numbers on the heatmap
                 fmt='.2f',
                 )
    ax.set_title('AIC')
    plt.show() 

手順3の一次差分を直接使って順序を固定すると、図のような結果になります。

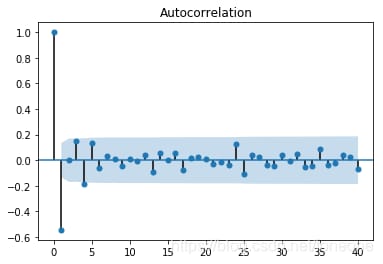
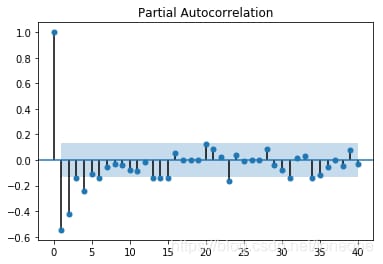
上のグラフはそれぞれACFとPACFのもので、順序がどのように決定されるかについては詳しく説明されていない。通常、順序は末尾を切り捨てて末尾にすることで決定される。

ヒートマップの順番を決定した結果は以下の通りです。

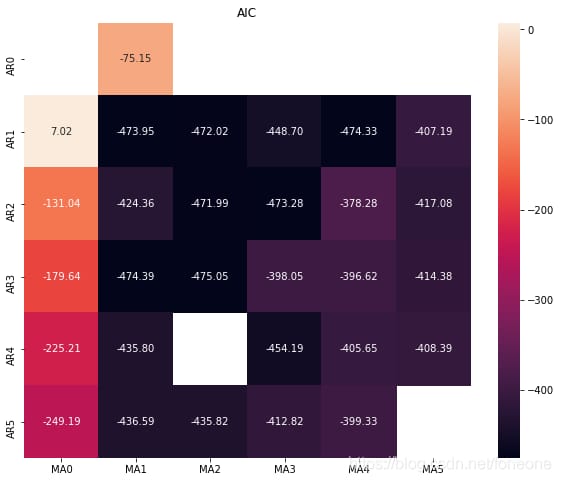
黒の位置は、p、qが（1，1）（3，1）（1，4）を取ることが問題ないことを確認するのがベストです。一般に小さいほど良い。

ヒートマップの実装方法は記事で参照していますが、ブログのリンクが抜けているので、もし侵害があればご連絡いただければ該当箇所を削除します。

ステップ6：モデルの構築

def ARMA_model(train_data,order): # Training data, test data, fixed order
    arma_model = ARMA(train_data,order) # ARMA model
    arma = arma_model.fit() # activate the model
    #print(result.summary()) #give a model report
    
    ############ in-sample ############ in-sample prediction 
    in_sample_pred = arma.predict()

    ############ out-sample ########## out-of-sample prediction
    #### out-sample prediction needs to start at a time point within the train_data sample
    #### use start and end to control the out-of-sample prediction start and end times
    out_sample_pred = arma.predict(start=len(train_data)-2,end = len(train_data)+30, \
                              dynamic=True) 
    #in_sample_pred.plot()
    #train_data.plot()
    return arma,in_sample_pred,out_sample_pred
 
def ARIMA_model(train_data,order):
    arima_model = ARIMA(train_data,order) #ARIMA model
    arima = arima_model.fit()
    #print(result.summary()) #give a report of the model
    
    ######## in_sample_prediction #########
    in_sample_pred = arima.predict()


    ####### out_sample_predict ##########
    out_sample_pred = arima.predict(start=len(train_data)-2,end = len(train_data)+30, \
                              dynamic=True)

    return arima,in_sample_pred,out_sample_pred

予測処理には2種類あり、1つは サンプル内予測(in_sample_pred) と、もうひとつは サンプル外予測(out_sample_pred) . サンプル内予測は、2018-1-1～2018-8-1までのものです。しかし、予測するケースが8-1から9-1であるのはアウトサンプル予測であり、一般的にはインサンプル予測ではなく、アウトサンプルが欲しいところです。

サンプル外予測は、ダイナミックパラメータ には特に注意してください。 : サンプル外の予測は、同様にサンプル内のある時点からしか行えません。したがって サンプル外予測はtrain_dataの長さ内のある時点から開始されます．

ステップ7：モデルの評価

主に4つの方法があります。(残差が正規分布を満たすかどうかを調べるQQプロット ②残差の自己相関を調べるD-W検定 ③予測値と真値の標準偏差、誤差相関などを計算する。(4) 予測系列とテスト系列を縮小し、そのプロットを用いてモデルを視覚的に評価すること

def evaluate_model(model,train_data,predict_data):
    
    ###(1) Use QQ plots to test if the residuals satisfy a normal distribution
    resid = model.resid # Solve for the model residuals
    plt.figure(figuresize=(12,8))
    qqplot(residid,line='q',fit=True)

    ### (2) using the D-W test, test the autocorrelation of the residuals
    print('D-W test value is {}'.format(durbin_watson(residid.values)))

    ### (3) Error detection using predicted and true values, here the standard deviation is used
    ###row_train_data is from 2018-1-1,after differencing train_data changes
    print('standard deviation is {}'.format(mean_squared_error(train_data,predict_data,sample_weight=None,\
        multioutput='uniform_average'))) #standard_deviation (mean_squared_error)


def string_toDatetime(string): # intercept time
    return datetime.datetime.strptime(string, "%Y-%m-%d %H:%M:%S")

#### draw_picture,view_prediction
def draw_picture(row_train_data,out_sample_pred,test_data): 
    #print(out_sample_pred)
    # out-of-sample_prediction passed in test_data,out_sample_pred
    # Since the predictions are derived from the differenced smooth series, it is necessary to restore the differenced data
    # Plot the curve from the same starting point after reduction

    ####### restore out_sample_pred #########
    #### out_sample 2018-07-31 
    #### test_data 2018-8-1
    
    ##2018-8-1 00:00 to 2018-9-1 00:00 ###
    ## Restore the differenced sequence,re_out_sample_pred is after the reduction
    re_out_sample_pred = pd.Series(np.array(row_train_data)[-2][0],\
         index=[row_train_data.index[-2]]).append(out_sample_pred[1:]).cumsum()
   
    
    #### horizontal coordinates 
    x = []
    for i in range(32):
        x.append(i+1)
    x = np.array(x)
    
    #### vertical coordinates
    y1 = np.array(test_data)
    y2 = np.array(re_out_sample_pred[1:])
    
    #### Draw the plot
    plt.plot(x,y1,color='blue')
    plt.plot(x,y2,color='red')
    plt.show()

(1) qqプロットは以下のようになります。                   

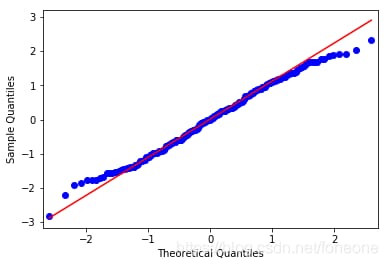
           qqプロットでは、残差はほぼ正規分布を満たしていることがわかる。

(2) D-W検定の結果は。

         D-W検定の値が2に近い場合、自己相関がなく、より良いモデルであることを示している。

         D-W検定がどのように機能するかの数学的な説明は、以下のリンクで見ることができます。

DW値判断のガイドライン - 百度文庫

(3) 標準偏差を用いたモデルを評価する場合、特に標本外予測では、時系列のタイムアライメントに注意する。

予測データを減らすためにグラフを使用して、cumsumum()関数の主な使用は、主な役割は、累積演算です。

  re_out_sample_pred = pd.Series(np.array(row_train_data)[-2][0],\
         index=[row_train_data.index[-2]]).append(out_sample_pred[1:]).cumsum()

   上記のステップ関数を呼び出すコードは以下の通りです。

if __name__ == "__main__":
    ## Step 1 and Step 2 both run only once
    genertate_data() # Generate data
    data_preprocessing() # 1: data preprocessing 
    train_data,test_data = Resampling() #:2: data resampling, return training data and test data
    row_train_data = train_data # Save the sequence before differencing, for evaluation later
    ### Difference or rolling average, determined using step 4 function
    Smooth_data = stationarity(train_data) # 4 differencing

    for data in zip(Smooth_data,range(4)):# range(4) to determine which method satisfies smoothness and white noise  
        if ADF_test(data[0]) and random_test(data[0]) : # Smoothness and white noise detection
            train_data = data[0] # first use differencing, then smoothing, for each of the 4 sequences
            method = data[1]
            print(method) #### If it is done by differencing, then this parameter should be used later in the ARIMA model
            break 
    ## Choose one of the three
    determinate_order_acf(train_data) # ACF determinate order
    detetminante_order_AIC(train_data) # BIC order
    heatmap_AIC(train_data) # heatmap Display
    #### model proposal and model evaluation
    #### order is given by difference and fixed order
    order = (1,1) ## ARMA p,q
    order = (2,1,0) ## ARIMA p,d,q
    #### Call the model
    arma,in_sample_pred,out_sample_pred = ARMA_model(train_data,order)
    arima,in_sample_pred,out_sample_pred = ARIMA_model(train_data,order)
    
    #### model evaluation (both in-sample and out-sample, only in-sample is used here)
    evaluate_model(arma,train_data,in_sample_pred) # in-sample prediction
    evaluate_model(arima,train_data,in_sample_pred) # in-sample prediction
   
    #### draw_picture-variance_comparison (out-of-sample_prediction)
    draw_picture(row_train_data,out_sample_pred,test_data)

概要

ARMA、ARIMAモデルについては、データ処理から最終的なモデリング実装まで行う。

しかし、実はそこには大きな問題があって、データが滑らかなデータでない場合、処理に差分法が使われ、dropna()という関数を使って、系列からナン（この場合は0）を削除することになっています。つまり、系列内の隣り合う2列が等しい場合、前の列を削除するため、処理後のデータは各日のデータに従って分布していないかもしれませんが、予測値は各日とも存在します。

dropna()関数を追加しないと、固定オーダーのものはエラーを報告しますが（エラーメッセージはnan値があるというもの）、モデルのほうはエラーを報告しません。ということで、これは対策が必要な問題なのですが、あまり深入りしていないような記事も多いので、このあたりはどうなんでしょうか。

ブログ全体はコード実装で、具体的な数式はBaiduにありますよ〜〜〜。

2022年1月5日に更新しました。

このバージョンのコードは、statsmodels 0.10.1の実装に基づいています。最新版のstatsmodelsでは、以下のようなARMA、ARIMAモデルは呼び出せなくなりました。

from statsmodels.tsa.arima_model import ARIMA #ARIMA model
from statsmodels.tsa.arima_model import ARMA #ARMA model

新しいバージョンは

from statsmodels.tsa.arima.model import ARIMA #ARIMA model

ARMAは他のモジュールに包まれているようなので、ARMAモデルを使って議論したい場合は、ウェブサイトを確認する必要があります。

記事の長さの関係で、コードのフルバージョンは以下の公開番号に同期され、質問と返信を先にサポートします。お気軽にフォローしてください。