ツリー構造データベースのテーブルのスキーマ設計のための2つのオプション

2022-01-17 02:18:53

プリアンブル

プログラミングの過程で、企業の階層部門、列構造、商品分類など、あるデータに関連する関係を特徴づけるために、木構造を使うことがよくあります。通常、これらのツリー構造を完成させるには、データベースの助けを借りて永続化する必要がある。しかし、リレーショナルベースのデータベースの現在の様々な、データ情報を格納するために2次元テーブルレコードの形で、それは直接DBMSにツリーではないので、適切なスキーマとその対応するCRUDアルゴリズムの設計は、キーは、木構造を格納するためにリレーショナルデータベースを実現するためのものです。

理想的なツリー構造は、データ保存の冗長性が小さく直感的、検索トラバーサル処理がシンプルで効率的、ノードの追加・削除・チェックのCRUD操作が効率的といった特徴を備えている必要があります。うっかり非常に巧妙なデザインを見つけるために、インターネット上で検索すると、元は英語ですが、それを読んで、少し面白いと感じるので、彼らは少し整理した。この記事では、ツリー構造の2つのSchemaの設計ソリューションを紹介します：一つは直感的でシンプルなデザインのアイデアであり、もう一つは、左右の値のコーディングに基づいて、改善されたソリューションです。

I. 基本データ

本稿では、食品の系譜の一例として、食品をカテゴリー、色、品種ごとに整理し、以下のような木構造図にして説明する。

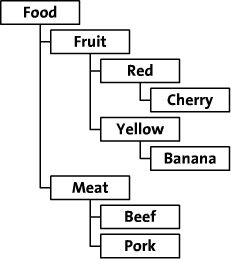
II. 継承駆動型スキーマ設計

ツリー構造の最も直感的な分析は、ノード間の継承関係であり、ノードの親ノードを表示することにより、2次元の関係表を確立できるように、この方式のツリーテーブル構造は、通常次のように設計されています。{Node_id,Parent_id}、上記のデータは、次のように記述することができます。

このソリューションの利点は明白です。デザインと実装が自然で、非常に直感的で使いやすいのです。ノード間の継承関係が直接文書化されているため、ツリーに対するCRUD操作は非効率的で、主に頻繁なquot;recursive"操作により、再帰的プロセスが常にデータベースにアクセスし、データベースIOごとに時間のオーバーヘッドが発生します。もちろん、この解決策は無駄ではありません。比較的小さなTreeの場合、最適化を行うためにキャッシュメカニズムを使用し、Treeの情報をメモリにロードして処理することで、直接データベースIO操作のパフォーマンスオーバーヘッドを回避することができます。

III. 左右の値エンコーディングに基づくスキーマ設計

一般的なデータベースベースのアプリケーションでは、削除や修正よりも問い合わせの必要性が常に高くなる。そこで、木構造のデータを保存するために、Treeの前置トラバーサルに基づく無限グループ化左・右エンコーディング方式による非再帰的な問い合わせを新たに設計する。

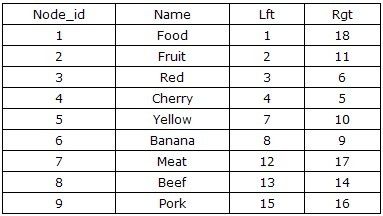
初めてこのテーブル構造を見た人は、左の値（Lft）と右の値（Rgt）がどのように計算されているのか分からない人がほとんどだと思いますし、このテーブルデザインでは親ノードと子ノードの継承関係が保たれていないように思います。しかし、テーブルの数字を指で指して1から18まで数えると、何かが見つかるはずですよね？そう、指を動かす順番は、下の図のように、木がプレオーダーでトラバースされる順番になるのです。ルートノードFoodの左側から始めて、1という印をつけ、プレオーダー・トラバースの方向にトラバーサルパスの数字をマークしていくと、最終的にルートノードFoodに戻り、右側に18と書き込むことができます。

この表構造を初めて見たとき、左の値（Lft）と右の値（Rgt）がどのように計算されているのか分からない人がほとんどだと思いますし、この表デザインは親ノードと子ノードの継承関係が保たれていないように見えます。しかし、テーブルの数字を指で指して1から18まで数えてみると、何かが見つかるはずですよね？そう、指を動かす順番は、下の図のように、木がプレオーダーでトラバースされる順番なのです。ルートノードFoodの左側から始めて、1という印をつけ、プレオーダー・トラバースの方向にトラバーサルパスの数字をマークしていくと、最終的にルートノードFoodに戻り、右側に18と書き込むことができます。

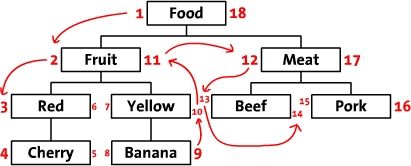
この設計から、左の値が2以上、右の値が11以下のノードはすべてFruitの後継ノードであり、左と右の値によって木全体の構造が保存されていると推論できる。しかし、これだけでは不十分で、CRUDを実行できることが目標である。

(1) あるノードの子孫ノードを取得する

前置走査でノードの子や孫のリストを返すために必要なSQL文は1つだけである。SELECT* FROM Tree WHERE Lft BETWEEN 2 AND 11 ORDER BY Lft ASC。クエリの結果は以下のようになります。

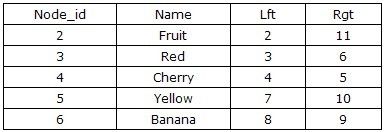
では、1つのノードには何人の子供がいるのでしょうか？ノードの左右の値を使って、その子孫を丸で囲むと、子孫の総数＝（右の値-左の値-1）÷2となります。フルーツの場合、子孫の総数は (11 - 2 - 1) / 2 = 4. 木構造をより視覚的に表現するためには、そのノードが木構造のどのレベルに位置するかを知る必要がある。SELECTCOUNT(*) FROM Tree WHERE Lft <= 2 AND Rgt >= 11. 説明を簡単にするために、Tree用のビューを作成し、階層カラムを追加し、以下の関数定義でカスタム関数を記述することでカラムの値を計算することができます。

CREATE FUNCTION dbo.CountLayer
(
    @node_id int
)
RETURNS int
AS
begin
	declare @result int
	set @result = 0
	declare @lft int
	declare @rgt int
	if exists(select Node_id from Tree where Node_id = @node_id)
	begin
		select @lft = Lft, @rgt = Rgt from Tree where node_id = @node_id
		select @result = count(*) from Tree where Lft <= @lft and Rgt >= @rgt
	end
	return @result
end
GO

階層計算機能をベースに、レコードノードの階層を新たに配列として追加するビューを作成します。

CREATE VIEW dbo.
AS
SELECT Node_id, Name, Lft, Rgt, dbo.CountLayer(Node_id) AS Layer FROM dbo.
GO

与えられたノードのすべての子と対応する階層を計算するプロシージャを作成します。

CREATE PROCEDURE [dbo]. [GetChildrenNodeList]
(
	@node_id int
)
AS
declare @lft int
declare @rgt int
if exists(select Node_id from Tree where node_id = @node_id)
	begin
		select @lft = Lft, @rgt = Rgt from Tree where Node_id = @node_id
		select * from TreeView where Lft between @lft and @rgt order by Lft ASC
	end
GO

さて，上記のストアドプロシージャを使って，ノードFruitのすべての子孫ノードとそれに対応する階層を計算すると，クエリの結果は以下のようになります．

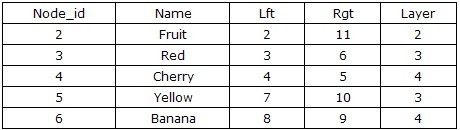
上記の実装から、左右のエンコーディング設計により、ツリーを走査するのに必要なデータベースクエリは2つだけで、再帰性が排除され、クエリ条件はすべて数値比較であり、クエリは非常に効率的であることがわかります。もちろん、ここではノードの子ノードを取得する簡単なアルゴリズムを示しただけで、このツリーの実際の利用には、同じレベルの翻訳ノードの挿入や削除などの機能を実装する必要があります。

(2) ノードの系譜を取得する

ノードの系譜を取得する場合、Fruitを例にとると、左右の値から1つのSQL文だけで解析が完了する。SELECT* FROM Tree WHERE Lft < 2 AND Rgt > 11 ORDER BY Lft ASC 、比較的完全な手続きである。

CREATE PROCEDURE [dbo]. [GetParentNodePath]
(
	@node_id int
)
AS
declare @lft int
declare @rgt int
if exists(select Node_id from Tree where Node_id = @node_id)
	begin
		select @lft = Lft, @rgt = Rgt from Tree where Node_id = @node_id
		select * from TreeView where Lft < @lft and Rgt > @rgt order by Lft ASC
	end
GO

(3) ノードに子ノードを追加する

例えば、quot;Red" というノードの下に新しい子ノード "Apple" を追加したいとすると、ツリーは次の図のようになり、赤いノードが新しいノードとなります。

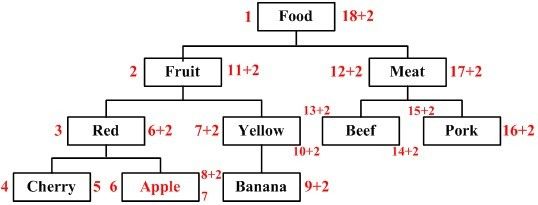
グラフのノード周辺の値の変化を注意深く見ていくと、SQLスクリプトをどう書けばいいのか、みんな推理できるはずです。子ノードを挿入するための比較的完全なストアドプロシージャを以下のように与えることができます。

CREATE PROCEDURE [dbo]. [AddSubNode]
(
	@node_id int,
	@node_name varchar(50)
)
AS
declare @rgt int
if exists(select Node_id from Tree where Node_id = @node_id)
	begin
		SET XACT_ABORT ON
		BEGIN TRANSCTION
		select @rgt = Rgt from Tree where Node_id = @node_id
		update Tree set Rgt = Rgt + 2 where Rgt >= @rgt
		update Tree set Lft = Lft + 2 where Lft >= @rgt
		insert into Tree(Name, Lft, Rgt) values(@node_name, @rgt, @rgt + 1)
		COMMIT TRANSACTION
		SET XACT_ABORT OFF
	end
GO

(4) ノードの削除

あるノードを削除したい場合、そのノードの子ノードをすべて同時に削除することになりますが、この削除されたノードの個数は (削除したノードの右の値 - 削除したノードの左の値 + 1) / 2 となり、残りのノードの左右の値が削除したノードの左右の値より大きい場合は調整されます。ツリーに何が起こるかを見るために、Beefを例にとると、削除の効果は下図のようになります。

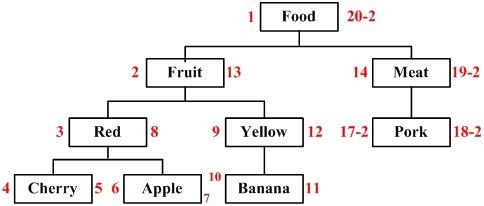
そして、対応するストアドプロシージャを構築することができます。

CREATE PROCEDURE [dbo]. [DelNode]
(
	@node_id int
)
AS
declare @lft int
declare @rgt int
if exists(select Node_id from Tree where Node_id = @node_id)
	begin
		SET XACT_ABORT ON
		BEGIN TRANSCTION
			select @lft = Lft, @rgt = Rgt from Tree where Node_id = @node_id
			delete from Tree where Lft >= @lft and Rgt <= @rgt
			update Tree set Lft = Lft - (@rgt - @lft + 1) where Lft > @lft
			update Tree set Rgt = Rgt - (@rgt - @lft + 1) where Rgt > @rgt
			COMMIT TRANSACTION
		SET XACT_ABORT OFF
	end
GO

V. 概要

この左右の値を符号化することで無限グループ化するツリー構造のSchema設計方式を次のようにまとめることができる。

(1) メリット：再帰的な操作を排除して無限グループ化を実現し、問い合わせ条件も定形数値の比較で済むため、非常に効率的である。

(2) デメリットノードの追加、削除、変更にコストがかかり、テーブル内のデータの多くの面を変更することになる。

もちろん、この記事では、CRUDアルゴリズムのより一般的な実装のいくつかを与える、我々はまた、同じレベルで、ノードの変換、ノードダウン、ノードアップなど、独自の操作を追加することができます。もし興味があれば、自分で実装をコーディングすることができますので、ここではリストアップしません。なお、これらのアルゴリズムの実装は、多くのupdate文を順次実行することになり、面倒なことになるかもしれません。逐次スケジューリングがうまくいかないと、バグによって木構造テーブル全体が憂慮すべきダメージを受けることになる。したがって、木構造に大規模な変更を加える場合は、一時テーブルを仲介してコードの複雑さを軽減し、万一に備えて変更を加える前にテーブルの完全なバックアップを取ることを強くお勧めします。クエリベースのデータベースアプリケーションの大部分では、親子継承関係で構築された従来のデータベーススキーマよりも、このスキーマの方が適用可能である。

ツリー構造データベースのテーブルのスキーマ設計についての説明は以上です。ツリー構造データベースのテーブルのスキーマ設計に関するより詳しい情報は、BinaryDevelopの過去の記事を検索するか、以下の関連記事を引き続きご覧ください。

参考を参照してください。データベースに階層的なデータを格納する記事一覧記事