質問

2次元のフィールド（軸x、y）を表現する必要があるのですが、1次元配列と2次元配列のどちらを使うべきかという問題に直面しています。

1次元配列（y + x*n）のインデックスを再計算することは、2次元配列（x、y）を使用するよりも遅くなる可能性があることは想像できますが、1次元はCPUキャッシュになる可能性があることは想像できます...。

いくつかググってみましたが、静的配列に関するページしか見つかりませんでした（そして、1Dと2Dは基本的に同じであることを述べています）。しかし、私の配列は動的でなければなりません。

だから、何ですか？

1. より高速になりました。
2. より小さい (RAM)

ダイナミック1Dアレイかダイナミック2Dアレイか？

どのように解決するのですか？

tl;dr : おそらく一次元のアプローチを使用する必要があります。

注意: 動的 1 次元または動的 2 次元のストレージ パターンを比較する場合、コードのパフォーマンスは非常に多くのパラメーターに依存するため、本を埋めることなくパフォーマンスに影響する詳細を掘り下げることはできません。可能であれば、プロファイルを作成してください。

1. 何が速いか？

密な行列の場合、1次元のアプローチは、より良いメモリ局所性と少ない割り当てと割り当て解除のオーバーヘッドを提供するので、より速くなる可能性が高いです。

2. 何がより小さいか？

Dynamic-1Dは、2Dアプローチよりも少ないメモリを消費します。後者はまた、より多くの割り当てを必要とします。

備考

以下に、いくつかの理由とともに、かなり長い答えを並べましたが、まず、あなたの前提について、いくつか指摘したいと思います。

1次元配列（y + x*n）のインデックスを再計算すると、2次元配列（x、y）を使用するよりも遅くなる可能性があることを想像することができます。

この2つの関数を比較してみましょう。

int get_2d (int **p, int r, int c) { return p[r][c]; }
int get_1d (int *p, int r, int c)  { return p[c + C*r]; }

これらの関数に対してVisual Studio 2015 RCが生成した（最適化をオンにした）（非インライン化）アセンブリは次のとおりです。

?get_1d@@YAHPAHII@Z PROC
push    ebp
mov ebp, esp
mov eax, DWORD PTR _c$[ebp]
lea eax, DWORD PTR [eax+edx*4]
mov eax, DWORD PTR [ecx+eax*4]
pop ebp
ret 0

?get_2d@@YAHPAPAHII@Z PROC
push ebp
mov ebp, esp
mov ecx, DWORD PTR [ecx+edx*4]
mov eax, DWORD PTR _c$[ebp]
mov eax, DWORD PTR [ecx+eax*4]
pop ebp
ret 0

差分は mov (2d)に対して lea (1d). 前者はレイテンシ3サイクル、最大スループット2/サイクルで、後者はレイテンシ2サイクル、最大スループット3/サイクルとなります。(以下 命令表 - アグネル・フォグ この違いは微々たるものなので、インデックスの再計算に起因する大きな性能差は発生しないはずだと考えています。この差自体がボトルネックになっていることを特定することは、どのプログラムでも非常に少ないと予想されます。

これは次の（そしてより興味深い）ポイントにつながります。

...しかし、私は1DがCPUキャッシュにある可能性を想像することができました....

確かに、でも2DもCPUキャッシュにある可能性がありますね。以下を参照してください。 欠点 メモリの局所性 を参照してください。

長い答え、つまり動的な 2 次元データ ストレージ (pointer-to-pointer または vector-of-vector) が以下のように悪い理由です。 シンプル / 小さい行列に適していません。

注意: これは動的な配列/割り当てスキーム [malloc/new/vector など] についてです。静的な 2 次元配列は連続したメモリ ブロックであるため、ここで紹介する欠点には当てはまりません。

問題点

動的配列の動的配列、またはベクトルのベクトルが、なぜデータストレージとして適していないのかを理解するために、そのような構造のメモリレイアウトを理解する必要があります。

ポインタからポインタへの構文を使用する場合の例

int main (void)
{
    // allocate memory for 4x4 integers; quick & dirty
    int ** p = new int*[4];
    for (size_t i=0; i<4; ++i) p[i] = new int[4]; 

    // do some stuff here, using p[x][y] 

    // deallocate memory
    for (size_t i=0; i<4; ++i) delete[] p[i];
    delete[] p;
}

デメリット

メモリローカリティ

この「行列」のために、4つのポインタの1ブロックと4つの整数の4ブロックを割り当てます。 すべての割り当ては関連性がありません であるため、任意のメモリ位置になる可能性があります。

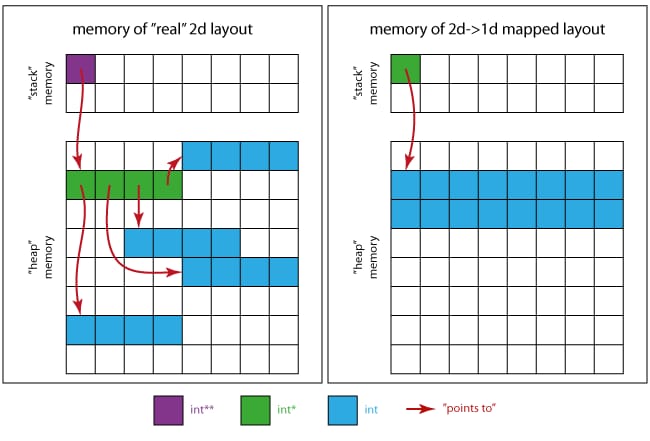
次の画像は、メモリがどのように見えるかのアイデアを与えてくれるでしょう。

については 実際の2次元の場合 :

• 紫色の四角は、メモリの位置を占有している p そのものです。
• 緑色の四角は、メモリ領域を組み立てる p を指しています（4 x int* ).
• の指す4つの領域は、連続した青い四角形で、それぞれ int* 緑色の領域の

については 1次元のケースに2次元をマッピング :

• 緑色の四角は、唯一必要なポインタです int *
• 青い四角は、すべての行列要素用のメモリ領域を組み立てます（16 x int ).

これは、（左のレイアウトを使用する場合）おそらく、キャッシュなどのために、（右のように）連続したストレージ パターンの場合よりもパフォーマンスが低下することを意味します。

キャッシュ ラインが一度にキャッシュに転送されるデータ量であるとし、プログラムが行列全体に 1 つの要素を次々にアクセスすることを想像してみましょう。

32 ビット値の 4 x 4 行列が適切に配置されている場合、64 バイトのキャッシュ ライン (一般的な値) を持つプロセッサは、データ (4*4*4 = 64 バイト) をワンショットで処理することが可能です。 処理を開始したときにデータがまだキャッシュにない場合、キャッシュミスに直面し、データがメインメモリからフェッチされます。このロードは、行列が連続的に格納されている（かつ、適切にアラインされている）場合に限り、キャッシュラインに収まるので、行列全体を一度にフェッチすることができます。 そのデータを処理する間、おそらくこれ以上のミスはないでしょう。

各行/列の関連性のない場所を持つ動的なリアル 2 次元システムの場合、プロセッサはすべてのメモリ場所を別々にロードする必要があります。 必要なのは64バイトだけですが、4つの無関係なメモリ位置に対して4つのキャッシュラインをロードすると、最悪の場合、実際には256バイトを転送し、75%のスループット帯域幅を浪費することになります。 2d スキームを使用してデータを処理する場合、（まだキャッシュされていない場合）最初の要素でキャッシュミスに直面することになります。 しかし今度は、メインメモリから最初にロードされた後、最初の行/列だけがキャッシュに残ります。他の行はすべてメモリ内の他の場所にあり、最初の行に隣接していないからです。 新しい行/列に到達するとすぐに、再びキャッシュミスが発生し、メインメモリから次のロードが実行されます。

長い話を端折ると、2d パターンはキャッシュミスの可能性が高く、1d スキームはデータの局所性によりパフォーマンスの可能性が高いということです。

頻繁な割り当て/解放

• 何度でも N + 1 (4 + 1 = 5) の割り当てが (new, malloc, allocator::allocate などのいずれかを使用して) 目的の NxM (4×4) 行列を作成するために必要です。
• 同じ数の適切な、それぞれの割り当て解除操作が同様に適用されなければなりません。

したがって、単一の割り当てスキームとは対照的に、そのような行列を作成/コピーすることはよりコストがかかります。

これは行の数が増えるにつれてさらに悪化します。

メモリ消費量オーバーヘッド

intは32ビット、ポインタは32ビットのサイズを想定しています。(注：システム依存です。)

思い出してみましょう。4×4のint型行列を格納したいので、64バイトということになります。

NxM行列をポインタからポインタへのスキームで格納する場合、以下のようになります。

• N*M*sizeof(int) [実際の青色データ] +
• N*sizeof(int*) [緑色のポインタ] +
• sizeof(int**) [紫色の変数p]バイト。

そのため 4*4*4 + 4*4 + 4 = 84 のバイトになり、さらに std::vector<std::vector<int>> . この場合 N * M * sizeof(int) + N * sizeof(vector<int>) + sizeof(vector<vector<int>>) のバイトで、つまり 4*4*4 + 4*16 + 16 = 144 バイトであり、4 x 4 intの64バイトとは別物です。

さらに、使用されるアロケータに依存しますが、各単一割り当てには、さらに 16 バイトのメモリ オーバーヘッドがあるかもしれません (ほとんどの場合、そうなるでしょう)。(適切な割り当て解除の目的で割り当てられたバイト数を保存する、いくつかの「Infobytes」)。

これは、最悪のケースを意味します。

N*(16+M*sizeof(int)) + 16+N*sizeof(int*) + sizeof(int**)

= 4*(16+4*4) + 16+4*4 + 4 = 164 bytes ! _Overhead: 156%_

オーバーヘッドのシェアは、マトリックスのサイズが大きくなるにつれて減少しますが、それでも存在します。

メモリリークのリスク

割り当ての束は、割り当ての1つが失敗した場合にメモリリークを回避するために適切な例外処理を必要とします! 割り当てられたメモリブロックを追跡する必要があり、メモリの割り当てを解除するときにそれらを忘れてはいけません。

もし new がメモリ不足になり、次の行を割り当てることができない場合（特に行列が非常に大きい場合に起こりがちです）。 std::bad_alloc がスローされます。 new .

例

上記の new/delete の例では、もし私たちが bad_alloc 例外が発生した場合の漏れを防ぎたい場合は、さらにコードが必要になります。

  // allocate memory for 4x4 integers; quick & dirty
  size_t const N = 4;
  // we don't need try for this allocation
  // if it fails there is no leak
  int ** p = new int*[N];
  size_t allocs(0U);
  try 
  { // try block doing further allocations
    for (size_t i=0; i<N; ++i) 
    {
      p[i] = new int[4]; // allocate
      ++allocs; // advance counter if no exception occured
    }
  }
  catch (std::bad_alloc & be)
  { // if an exception occurs we need to free out memory
    for (size_t i=0; i<allocs; ++i) delete[] p[i]; // free all alloced p[i]s
    delete[] p; // free p
    throw; // rethrow bad_alloc
  }
  /*
     do some stuff here, using p[x][y] 
  */
  // deallocate memory accoding to the number of allocations
  for (size_t i=0; i<allocs; ++i) delete[] p[i];
  delete[] p;

概要

本当の 2 次元メモリ レイアウトが適合し、意味をなす場合 (たとえば、行ごとの列の数が一定でない場合) もありますが、最も単純で一般的な 2D データ ストレージのケースでは、コードの複雑さを増大させ、プログラムのパフォーマンスとメモリ効率を低下させるだけです。

代替

連続したメモリブロックを使用し、そのブロックに行をマッピングする必要があります。

C++のやり方は、以下のような重要なことを考慮しながら、メモリを管理するクラスを書くことでしょう。

• 3 の法則とは何ですか?
• RAII（Resource Acquisition is Initialization）とはどういう意味ですか？
• C++の概念です。コンテナ (cppreference.com にて)

例

このようなクラスがどのように見えるかのアイデアを提供するために、いくつかの基本的な機能を持つ簡単な例を紹介します。

• 2 次元サイズ構成可能
• 2 次元サイズ変更可能
• operator(size_t, size_t) 2行の主要な要素にアクセスする場合
• at(size_t, size_t) チェックされた2行の主要な要素へのアクセスのため
• コンセプトの要件を満たす コンテナ

ソース

#include <vector>
#include <algorithm>
#include <iterator>
#include <utility>

namespace matrices
{

  template<class T>
  class simple
  {
  public:
    // misc types
    using data_type  = std::vector<T>;
    using value_type = typename std::vector<T>::value_type;
    using size_type  = typename std::vector<T>::size_type;
    // ref
    using reference       = typename std::vector<T>::reference;
    using const_reference = typename std::vector<T>::const_reference;
    // iter
    using iterator       = typename std::vector<T>::iterator;
    using const_iterator = typename std::vector<T>::const_iterator;
    // reverse iter
    using reverse_iterator       = typename std::vector<T>::reverse_iterator;
    using const_reverse_iterator = typename std::vector<T>::const_reverse_iterator;

    // empty construction
    simple() = default;

    // default-insert rows*cols values
    simple(size_type rows, size_type cols)
      : m_rows(rows), m_cols(cols), m_data(rows*cols)
    {}

    // copy initialized matrix rows*cols
    simple(size_type rows, size_type cols, const_reference val)
      : m_rows(rows), m_cols(cols), m_data(rows*cols, val)
    {}

    // 1d-iterators

    iterator begin() { return m_data.begin(); }
    iterator end() { return m_data.end(); }
    const_iterator begin() const { return m_data.begin(); }
    const_iterator end() const { return m_data.end(); }
    const_iterator cbegin() const { return m_data.cbegin(); }
    const_iterator cend() const { return m_data.cend(); }
    reverse_iterator rbegin() { return m_data.rbegin(); }
    reverse_iterator rend() { return m_data.rend(); }
    const_reverse_iterator rbegin() const { return m_data.rbegin(); }
    const_reverse_iterator rend() const { return m_data.rend(); }
    const_reverse_iterator crbegin() const { return m_data.crbegin(); }
    const_reverse_iterator crend() const { return m_data.crend(); }

    // element access (row major indexation)
    reference operator() (size_type const row,
      size_type const column)
    {
      return m_data[m_cols*row + column];
    }
    const_reference operator() (size_type const row,
      size_type const column) const
    {
      return m_data[m_cols*row + column];
    }
    reference at() (size_type const row, size_type const column)
    {
      return m_data.at(m_cols*row + column);
    }
    const_reference at() (size_type const row, size_type const column) const
    {
      return m_data.at(m_cols*row + column);
    }

    // resizing
    void resize(size_type new_rows, size_type new_cols)
    {
      // new matrix new_rows times new_cols
      simple tmp(new_rows, new_cols);
      // select smaller row and col size
      auto mc = std::min(m_cols, new_cols);
      auto mr = std::min(m_rows, new_rows);
      for (size_type i(0U); i < mr; ++i)
      {
        // iterators to begin of rows
        auto row = begin() + i*m_cols;
        auto tmp_row = tmp.begin() + i*new_cols;
        // move mc elements to tmp
        std::move(row, row + mc, tmp_row);
      }
      // move assignment to this
      *this = std::move(tmp);
    }

    // size and capacity
    size_type size() const { return m_data.size(); }
    size_type max_size() const { return m_data.max_size(); }
    bool empty() const { return m_data.empty(); }
    // dimensionality
    size_type rows() const { return m_rows; }
    size_type cols() const { return m_cols; }
    // data swapping
    void swap(simple &rhs)
    {
      using std::swap;
      m_data.swap(rhs.m_data);
      swap(m_rows, rhs.m_rows);
      swap(m_cols, rhs.m_cols);
    }
  private:
    // content
    size_type m_rows{ 0u };
    size_type m_cols{ 0u };
    data_type m_data{};
  };
  template<class T>
  void swap(simple<T> & lhs, simple<T> & rhs)
  {
    lhs.swap(rhs);
  }
  template<class T>
  bool operator== (simple<T> const &a, simple<T> const &b)
  {
    if (a.rows() != b.rows() || a.cols() != b.cols())
    {
      return false;
    }
    return std::equal(a.begin(), a.end(), b.begin(), b.end());
  }
  template<class T>
  bool operator!= (simple<T> const &a, simple<T> const &b)
  {
    return !(a == b);
  }

}

ここでいくつかのことに注意してください。

• T は、使用される要件を満たす必要があります。 std::vector メンバー関数
• operator() は範囲外のチェックを行いません。
• 自分でデータを管理する必要がない
• デストラクタ、コピーコンストラクタ、代入演算子不要

そのため、アプリケーションごとに適切なメモリ処理を悩む必要はなく、書いたクラスに対して一度だけ行うだけでよいのです。

制限事項

動的なquot;real"二次元構造が好ましい場合があります。たとえば、次のような場合です。

• 行列が非常に大きく、疎である場合（行のいずれかが割り当てられる必要がなく、nullptr を使用して処理できる場合）。
• 行が同じ数の列を持たない場合（つまり、行列ではなく、別の 2 次元構造体を持っている場合）。