[解決済み] 100個の動く標的の間の最短経路を見つけるには？(ライブデモを含む)

質問

背景

この画像は問題を説明するものです。

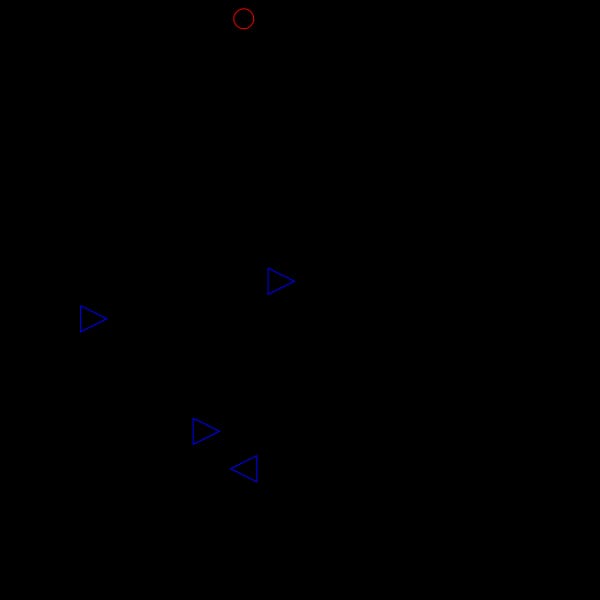
赤い丸はコントロールできる。 ターゲットは青い三角形です。 黒い矢印はターゲットが移動する方向を示しています。

最小のステップ数ですべてのターゲットを集めたい。

毎ターン、左右上下のどちらかに1歩ずつ移動しなければならない。

各ターン、ターゲットもボードに示された方向に従って1歩ずつ移動する。

デモ

この問題のプレイアブル・デモをアップしました。 ここでGoogle appengineに .

私の現在のアルゴリズムが最適でないことを示すので、誰かが目標スコアを破ることができれば、私は非常に興味を持つでしょう。 (これを達成した場合、おめでとうのメッセージが表示されるはずです!)

問題

私の現在のアルゴリズムは、ターゲットの数によって非常に悪くスケールします。 時間は指数関数的に増加し、16匹の魚のためにそれはすでに数秒です。

私は32*32のボードサイズと100の動くターゲットで答えを計算したいと思います。

質問内容

すべてのターゲットを収集するための最小ステップ数を計算するための効率的なアルゴリズム（理想的にはJavascriptで）は何ですか？

私が試したこと

私の現在のアプローチはメモ化に基づいていますが、非常に遅く、常に最適な解を生成できるかどうかはわかりません。

私は、「与えられたターゲットのセットを収集し、特定のターゲットに到達するための最小のステップ数は何か」というサブ問題を解きます。

この部分問題は、前に訪問したターゲットの各選択肢を調べることによって再帰的に解かれる。 私は、できるだけ早くターゲットの前のサブセットを収集し、その後、終了した位置からできるだけ早く現在のターゲットに移動することが常に最適であると仮定します（これが有効な仮定であるかどうかは分かりませんが）。

この結果、計算される状態は n*2^n となり、これは非常に急速に大きくなります。

現在のコードは以下の通りです。

var DX=[1,0,-1,0];
var DY=[0,1,0,-1]; 

// Return the location of the given fish at time t
function getPt(fish,t) {
  var i;
  var x=pts[fish][0];
  var y=pts[fish][1];
  for(i=0;i<t;i++) {
    var b=board[x][y];
    x+=DX[b];
    y+=DY[b];
  }
  return [x,y];
}

// Return the number of steps to track down the given fish
// Work by iterating and selecting first time when Manhattan distance matches time
function fastest_route(peng,dest) {
  var myx=peng[0];
  var myy=peng[1];
  var x=dest[0];
  var y=dest[1];
  var t=0;
  while ((Math.abs(x-myx)+Math.abs(y-myy))!=t) {
    var b=board[x][y];
    x+=DX[b];
    y+=DY[b];
    t+=1;
  }
  return t;
}

// Try to compute the shortest path to reach each fish and a certain subset of the others
// key is current fish followed by N bits of bitmask
// value is shortest time
function computeTarget(start_x,start_y) {
  cache={};
  // Compute the shortest steps to have visited all fish in bitmask
  // and with the last visit being to the fish with index equal to last
  function go(bitmask,last) {
    var i;
    var best=100000000;
    var key=(last<<num_fish)+bitmask;
    if (key in cache) {
      return cache[key];
    }
    // Consider all previous positions
    bitmask -= 1<<last;
    if (bitmask==0) {
      best = fastest_route([start_x,start_y],pts[last]);
    } else {
      for(i=0;i<pts.length;i++) {
        var bit = 1<<i;
        if (bitmask&bit) {
          var s = go(bitmask,i);   // least cost if our previous fish was i
          s+=fastest_route(getPt(i,s),getPt(last,s));
          if (s<best) best=s;
        }
      }
    }
    cache[key]=best;
    return best;
  }
  var t = 100000000;
  for(var i=0;i<pts.length;i++) {
    t = Math.min(t,go((1<<pts.length)-1,i));
  }
  return t;
}

私が考えたこと

私が考えた選択肢はいくつかあります。

1. 中間結果のキャッシュ 距離計算は多くのシミュレーションを繰り返すので、中間結果をキャッシュすることができる。
   
   しかし、これでは指数関数的な複雑さを持つことを止められないと思います。

2. 適切な許容ヒューリスティックが何であるか、そしてこれが実際にどのように効果的であるかは私には明らかではありませんが、A* 探索アルゴリズムです。

3. 巡回セールスマン問題に対する良いアルゴリズムを調査し、それらがこの問題に適用されるかどうかを確認すること。

4. この問題がNP困難であり、それゆえに最適解を求めることが不合理であることを証明しようとする。

どのように解決するのか？

文献を検索しましたか？私は、あなたの問題を分析していると思われるこれらの論文を見つけました。

• 動く標的の追跡と非定常巡回セールスマン問題"。 問題"。 http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.85.9940

• 移動目標巡回セールスマン問題(")。 http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.57.6403

UPDATE 1です。

上記2つの論文は、ユークリッド測度に対する線形移動に集中しているようです。