ロジスティック回帰のエラー問題：警告メッセージ。1: glm.fit: アルゴリズムが集約されていない 2: glm.fit: 適合率が0か1の値で計算されている

ロジスティック回帰のエラーメッセージには、以下の2つの問題があります。

警告: glm.fit: アルゴリズムは収束しませんでした。

警告: glm.fit: フィットした確率が数値的に0か1が発生しました。 

警告メッセージ

1: glm.fit: アルゴリズムが集計されない 

2: glm.fit: 適合率は0か1の値で計算されます。 

これはロジスティック回帰を行う際に比較的よくある問題で、なぜこのような問題が発生するのか、その例を紹介します。

まず、glm関数の紹介です。

glm(formula, family=family.generator, data,control = list(...))

ファミリーを使用します。各応答分布（指数分布のファミリー）は、平均と線形予測変数の関連付けを行うためのさまざまな関連付け関数を可能にします。

 よく使われるファミリ

binomal(link='logit') ---- 応答変数が、logitをリンク関数とする二項分布に従う、すなわち、ロジスティック回帰。

binomal(link='probit') ---- 応答変数がプロビット連結関数を持つ二項分布に従う。

poisson(link='identity') ---- 応答変数がポアソン分布に従う、すなわち、ポアソン回帰

control:制御アルゴリズムの誤差と最大反復回数

glm.control(epsilon = 1e-8, maxit = 25, trace = FALSE)  

     -----maxit:algorithm max iterations, change max iterations: control=list(maxit=100)

 glm関数は使用します。

library
("ggplot2")
data<-iris[1:100,]
samp<-sample(100,80)
names(data)<-c('sl','sw','pl','pw','species')
testdata<-data[samp,]
traindata<-data[-samp,]
lgst<-glm(testdata$species~pl,binomial(link='logit'),data=testdata)
## Warning: glm.fit: algorithm did not converge
## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
summary(lgst)
## 
## Call:
## glm(formula = testdata$species ~ pl, family = binomial(link = "logit"), 
## data = testdata)
## 
## Deviance Residuals: 
## Min 1Q Median 3Q Max  
## -2.202e-05 -2.100e-08 -2.100e-08 2.100e-08 3.233e-05  
## Coefficients: -2.202e-05 
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -97.30 87955.20 -0.001 0.999
## pl 39.56 34756.04 0.001 0.999
## (Dispersion) 
## (Dispersion parameter for binomial family taken to be 1)
## Null deviance: 1 
## Null deviance: 1.1045e+02 on 79 degrees of freedom
## Residual deviance: 2.0152e-09 on 78 degrees of freedom
## AIC: 4
## 
## Number of Fisher Scoring iterations: 25

lgst<-glm(testdata$species~pl,binomial(link='logit'),data=testdata,control=list(maxit=100))
## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
summary(lgst)
## 
## Call:
## glm(formula = testdata$species ~ pl, family = binomial(link = "logit"), 
## data = testdata, control = list(maxit = 100))
## 
## Deviance Residuals: 
## Min 1Q Median 3Q Max  
## -8.134e-06 -2.110e-08 -2.110e-08 2.110e-08 1.204e-05  
## Coefficients: -8.134e-06 
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -106.14 237658.98 0 1
## pl 43.16 93735.01 0 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## Null deviance: 1 
## Null deviance: 1.1070e+02 on 79 degrees of freedom
## Residual deviance: 2.7741e-10 on 78 degrees of freedom
## AIC: 4
## 
## Number of Fisher Scoring iterations: 27

lgst<-glm(testdata$species~pl,binomial(link='logit'),data=testdata,control=list(maxit=100))
## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
p<-predict(lgst,type='response')
qplot(seq(-2,2,length=80),sort(p),col='predict')

testdata$y <- c(1:80)
qplot(pl,y,data =testdata,colour =factor(species))

data<-iris[51:150,]
samp<-sample(100,80)
names(data)<-c('sl','sw','pl','pw','species')
testdata<-data[samp,]
traindata<-data[-samp,]
lgst<-glm(testdata$species~sw+pw,binomial(link='logit'),data=testdata)
summary(lgst)
## 
## Call:
## glm(formula = testdata$species ~ sw + pw, family = binomial(link = "logit"), 
## data = testdata)
## 
## Deviance Residuals: 
## Min 1Q Median 3Q Max  
## -1.68123 -0.12839 -0.01807 0.07783 2.24191  
 
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -12.792 5.828 -2.195 0.028168 *  
## sw -4.214 1.970 -2.139 0.032432 *  
## pw 15.229 3.984 3.823 0.000132 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Dispersion) 
## (Dispersion parameter for binomial family taken to be 1)
## (Dispersion parameter for binomial family taken to be 1) 
## Null deviance: 110.854 on 79 degrees of freedom
## Residual deviance: 21.382 on 77 degrees of freedom
## AIC: 27.382
## Number of Fisher Scoring it ## 
## Number of Fisher Scoring iterations: 7

なお、glm関数を用いてロジスティック回帰を実行すると、以下のような警告が表示されます。

警告メッセージ
1: glm.fit: アルゴリズムが集計されない 
2: glm.fit: 適合率は0か1の値として計算される

また、両係数のp値は0.999であり、回帰係数は有意でないことがわかる。

最初の警告：アルゴリズムが収束しない。
     glm関数のデフォルトの最大反復回数はmaxit=25です。データが良くない場合、25回反復してもアルゴリズムが収束しないことがあるので、反復回数を増やして収束しない問題を解決しようとします。しかし、反復回数を増やしてもアルゴリズムが収束しない場合は、データが本当に悪いので、特異値検定などのさらなるデータ処理が必要です。

p<-predict(lgst,type='response')
qplot(seq(-2,2,length=80),sort(p),col="response")

x3<-seq(1.5,4,length=80)
y3<-(4.284/15.656)*x3+13.447/15.656
aaa<-data.frame(x3,y3)

p <- ggplot()
p+geom_point(data = testdata,aes(x=sw,y=pw,colour=factor(species)))+
geom_line(data = aaa,aes(x = x3,y = y3,colour="line"))

summary(lgst)

## 
## Call:
## glm(formula = testdata$species ~ pl, family = binomial(link = "logit"), 
## data = testdata, control = list(maxit = 100))
## 
## Deviance Residuals: 
## Min 1Q Median 3Q Max  
## -8.134e-06 -2.110e-08 -2.110e-08 2.110e-08 1.204e-05  
## Coefficients: -8.134e-06 
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -106.14 237658.98 0 1
## pl 43.16 93735.01 0 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## Null deviance: 1 
## Null deviance: 1.1070e+02 on 79 degrees of freedom
## Residual deviance: 2.7741e-10 on 78 degrees of freedom
## AIC: 4
## 
## Number of Fisher Scoring iterations: 27

上記と同様に、最初の警告は反復回数を増やすことで解決し、その時点でアルゴリズムは収束する。

しかし、2つ目の注意点は残っており、回帰係数のP=1はまだ有意ではありません。

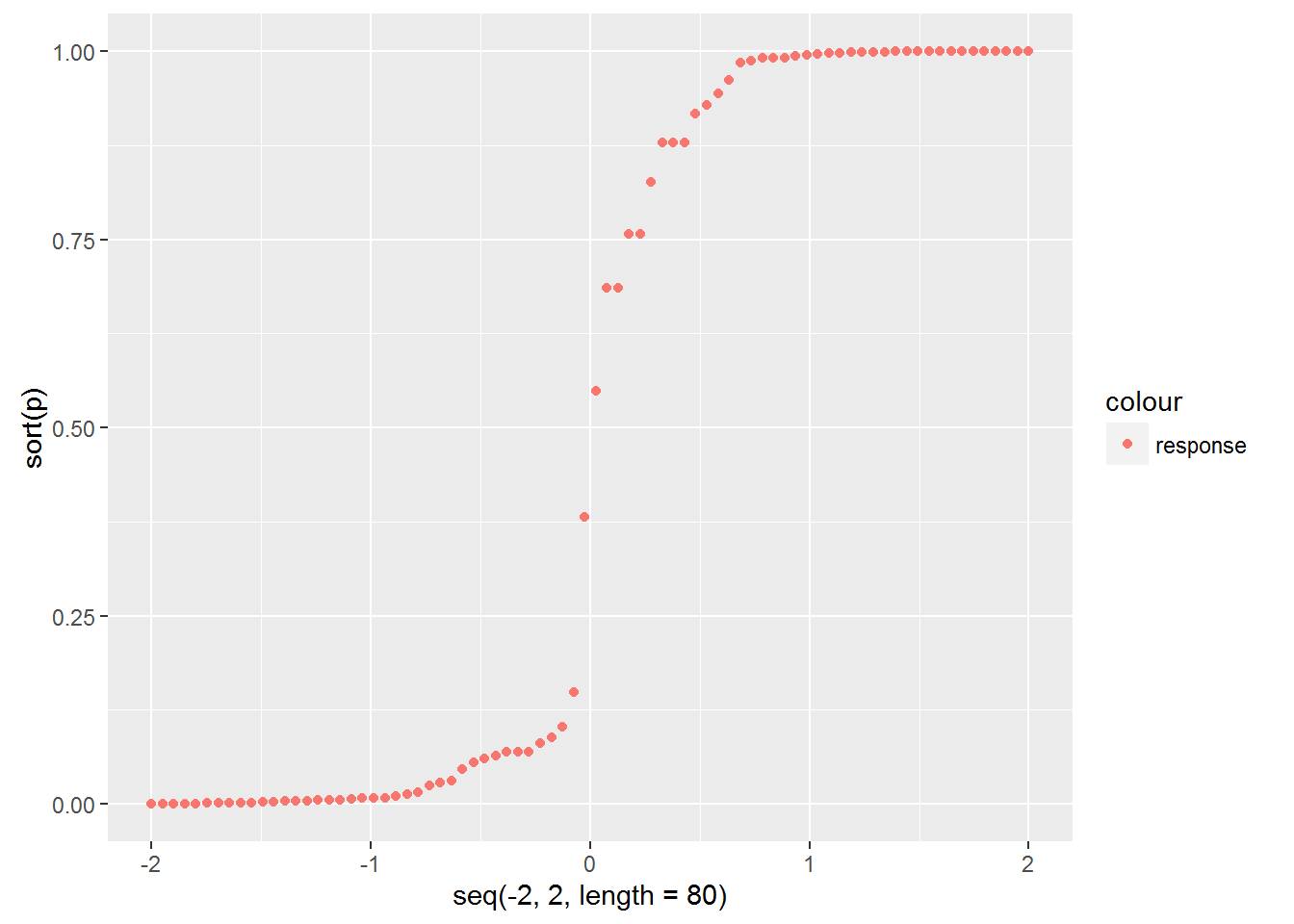
2つ目の警告：適合した確率は0か1になる

まず、この警告は何を意味するのでしょうか？
学習サンプルのロジスト回帰の結果を見てみましょう。適合した各サンプルが「セトーサ」クラスに属する確率は何％でしょうか？

lgst<-glm(testdata$species~pl,binomial(link='logit'),data=testdata,control=list(maxit=100))

## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

p<-predict(lgst,type='response')
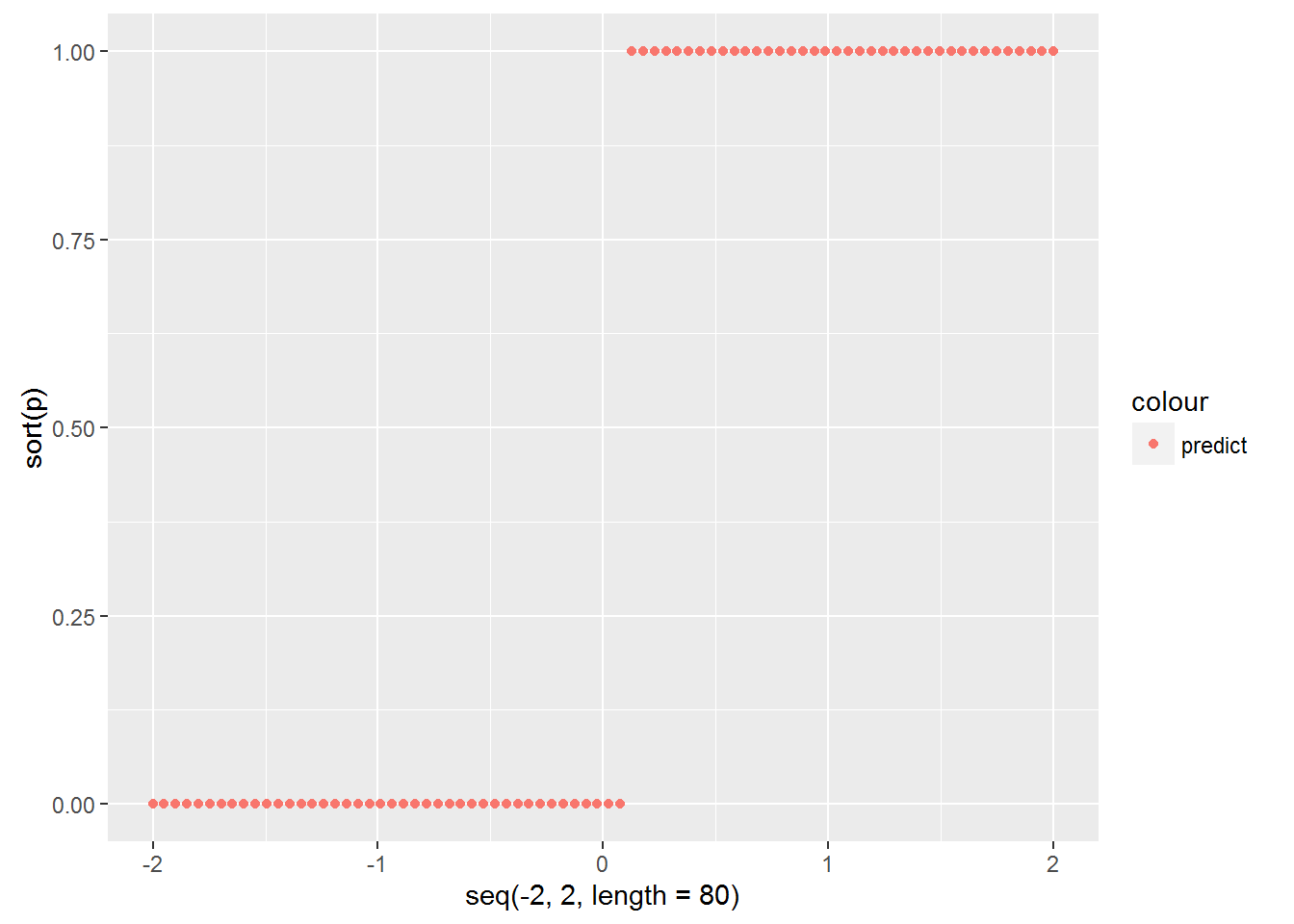
qplot(seq(-2,2,length=80),sort(p),col='predict')

<イグ

学習サンプルが「セトーサ」クラスである確率はほぼ0かほぼ1であり、ロジスティックモデルから予想されるS字カーブではないことがわかりますが、これが2つ目の注意点の意味するところです。

  では、なぜこのようなことが起こるのか、ということです。
 (以下は、いくつかの解説を参考にしながら、あくまで個人的な理解です）

  これは一種のオーバーフィットと解釈でき、データによる回帰係数の最適探索の過程で、ある種のカテゴリー（y=1）に対しては線形適合値が大きくなり、別の種のカテゴリー（y=0）に対しては小さくなる傾向があることを意味します。

回帰係数を解く際に大尤度推定の原理を用いるので、つまり、探索中に尤度関数が最大になるような回帰係数を求める：。

つまり、探索過程のバイアスは、y=1ではh(x)が大きくなり、y=0ではh(x)が小さくなる傾向があるのです。

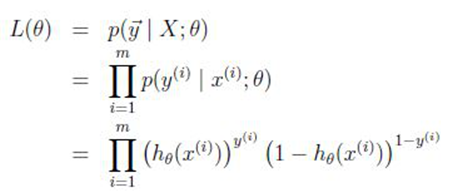
つまり、係数Θは、クラスY=1の-ΘTXを大きくし、クラスY=0の-ΘTXを小さくする傾向があるのです。そして、この結果、P(y=1|x;Θ)-->1; P(y=0|x;Θ)-->0 ...となります。

そこでまた疑問なのですが、どのようなデータであれば、このようなオーバーフィットが発生するのでしょうか？

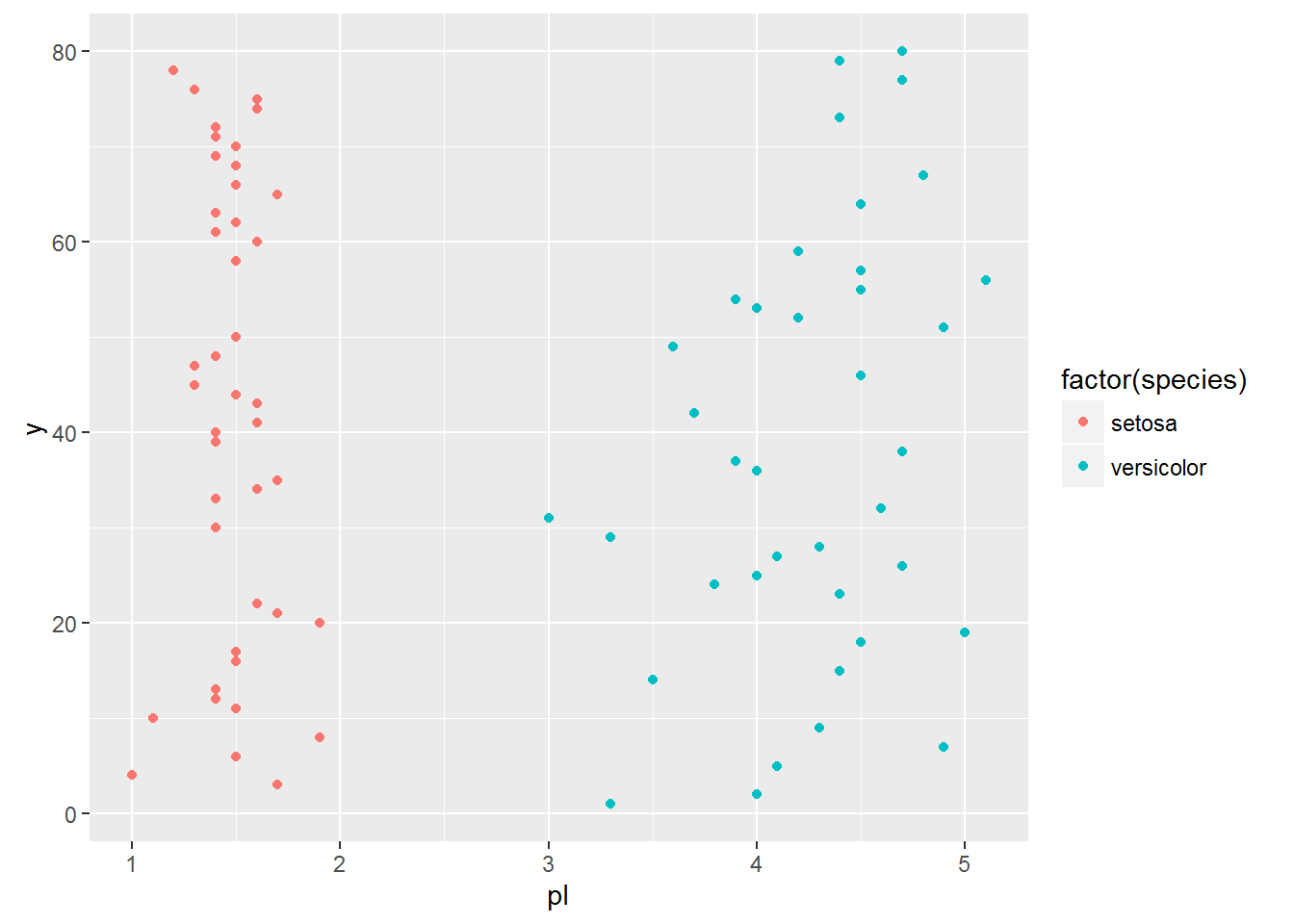
 まず、上のロジスティック回帰のサンプルpl値がsetosaとversicolorの場合を見てみましょう（横軸はpl値で、サンプルplのデータポイントが重ならないように、相関のないy値を加えてサンプルポイントを拡張しています）。

testdata$y <- c(1:80)
qplot(pl,y,data =testdata,colour =factor(species))

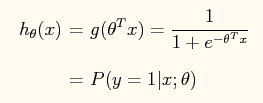
2種類のデータの完全な線形分離性が見て取れます。

したがって、回帰係数探索時に一変量線形関数h(x)の傾きの絶対値を大きくすることで、y=1クラスではh(x)を大きく、y=0クラスではh(x)を小さくできるのです。

つまり、サンプルデータが完全に分割可能な場合、ロジスティック回帰はしばしばオーバーフィットの問題、すなわち、フィットした確率が0か1になるように働くという2つ目の注意点が生じます。

このような線形分割可能なサンプルデータに対しては、ルールベースのアプローチを直接用いるのが、実はシンプルで応用が利くのです（例：pl<2.5ならセトーサクラス、pl>2.5ならバーシカロルクラス）。

以下、不完全に分離可能な2次元の学習データに対するロジスティック回帰の処理を示す。

data<-iris[51:150,]
samp<-sample(100,80)
names(data)<-c('sl','sw','pl','pw','species')
testdata<-data[samp,]
traindata<-data[-samp,]
lgst<-glm(testdata$species~sw+pw,binomial(link='logit'),data=testdata)
summary(lgst)

## 
## Call:
## glm(formula = testdata$species ~ sw + pw, family = binomial(link = "logit"), 
## data = testdata)
## 
## Deviance Residuals: 
## Min 1Q Median 3Q Max  
## -1.68123 -0.12839 -0.01807 0.07783 2.24191  
 
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -12.792 5.828 -2.195 0.028168 *  
## sw -4.214 1.970 -2.139 0.032432 *  
## pw 15.229 3.984 3.823 0.000132 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Dispersion) 
## (Dispersion parameter for binomial family taken to be 1)
## (Dispersion parameter for binomial family taken to be 1) 
## Null deviance: 110.854 on 79 degrees of freedom
## Residual deviance: 21.382 on 77 degrees of freedom
## AIC: 27.382
## Number of Fisher Scoring it ## 
## Number of Fisher Scoring iterations: 7

確率曲線グラフのあてはめ。(基本的にロジスティックモデルのS字カーブにフィットします。）

p<-predict(lgst,type='response')
qplot(seq(-2,2,length=80),sort(p),col="response")

学習用サンプルと分類境界の散布図。

(ロジスティック回帰の分類境界を描く、つまり曲線h(x)=0.5を描く)

x3<-seq(1.5,4,length=80)
y3<-(4.284/15.656)*x3+13.447/15.656
aaa<-data.frame(x3,y3)

p <- ggplot()
p+geom_point(data = testdata,aes(x=sw,y=pw,colour=factor(species)))+
geom_line(data = aaa,aes(x = x3,y = y3,colour="line"))

 内容は、本家ブログの方を参照し、印象を深めるために、自分でもう一度、図をggplot2に置き換え、本家参照は以下のように繋げました。

出典  http://www.cnblogs.com/runner-ljt/p/4574275.html